Введение
Наверняка многие из вас во время прохождения собеседования, на тестировании BrainBench или еще где-либо встречались с такой академической задачей, как обход графа наследования. Звучит задача проще: в какой последовательности будут вызываться конструкторы в представленной иерархии, и далее следует листинг. Естественно, решать эту задачу надо без использования компилятора. Итак, здесь я попытаюсь выделить некоторые правила по решению этой задачи. Условимся рисовать граф слева направо, т.е. если "A" наследует "B", а потом "C", то стрелка "AB" будет левее стрелки "AC". И еще… Перечислять порядок вызова конструкторов мы будем с конца - так легче.
Невиртуальное наследование
Рассмотрим для начала примеры на невиртуальное наследование.
Правило тут одно - главнее та ветвь, которая расположена правее
Листинг 1
#include<iostream> class A1 { public: A1(){std::cout << "A1 ";} }; class A2 { public: A2(){std::cout << "A2 ";} }; class B1: public A1 { public: B1(){std::cout << "B1 ";} }; class B2: public A2 { public: B2(){std::cout << "B2 ";} }; class C: public B1, public B2 { public: C(){std::cout << "C ";} }; class E: public C { public: E(){std::cout << "E ";} }; void main() { E *e = new E(); } |
На основе листинга получаем следующий граф
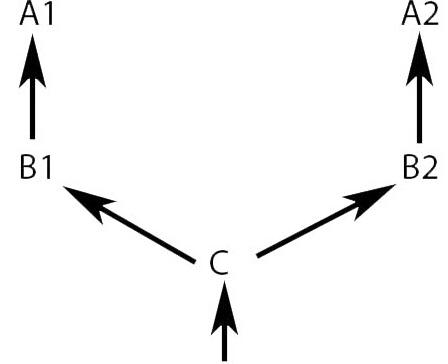
Начинаем обход, как я уже говорил, с конца. Сначала следует "E", затем в узле "C" применяем наше правило. Дойдя до конца, возвращаемся к узлу "C" (учитывать второй раз его не надо) и идем по левой ветви. Получилось "E C B2 A2 B1 A1". Инвертируем порядок - "A1 B1 A2 B2 C E"
Рассмотрим другой пример
Листинг 2
#include<iostream> class A1 { public: A1(){std::cout << "A1";} }; class A2 { public: A2(){std::cout << "A2";} }; class B1: public A1 { public: B1(){std::cout << "B1";} }; class B2: public A2 { public: B2(){std::cout << "B2";} }; class C: public B1, public B2 { public: C (){std::cout << "C";} }; class D1: public C { public: D1(){std::cout << "D1";} }; class D2: public C { public: D2(){std::cout << "D2";} }; class E: public D1, public D2 { public: E(){std::cout << "E";} }; void main() { E *e = new E(); } |
Получаем следующий граф
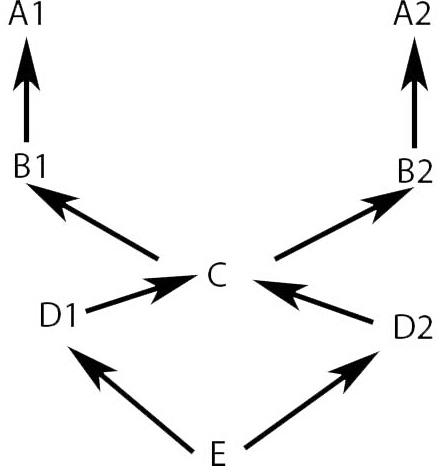
Начинаем, как обычно, с правой ветви - "E D2 C". Дойдя до "C", видим очередное разветвление. Применяем правило - "B2 A2 B1 A1". А теперь то же самое, но по левой ветви - "E" уже не учитываем, "D1 C". Дойдя до разветвления, применяем правило - "B2 A2 B1 A1". В итоге имеем - "E D2 C B2 A2 B1 A1 D1 C B2 A2 B1 A1". Инвертируем - "A1 B1 A2 B2 C D1 A1 B1 A2 B2 C D2 E"
Еще пример:
Листинг 3
#include<iostream> class G { public: G(){std::cout << "G";} }; class A1: public G { public: A1(){std::cout << "A1";} }; class A2: public G { public: A2(){std::cout << "A2";} }; class B1: public A1 { public: B1(){std::cout << "B1";} }; class B2: public A2 { public: B2(){std::cout << "B2";} }; class C1: public B1, public B2 { public: C1(){std::cout << "C1";} }; class D1: public C { public: D1(){std::cout << "D1";} }; class D2: public C { public: D2(){std::cout << "D2";} }; class E: public D1, public D2 { public: E(){std::cout << "E";} }; void main() { E *e = new E(); } |
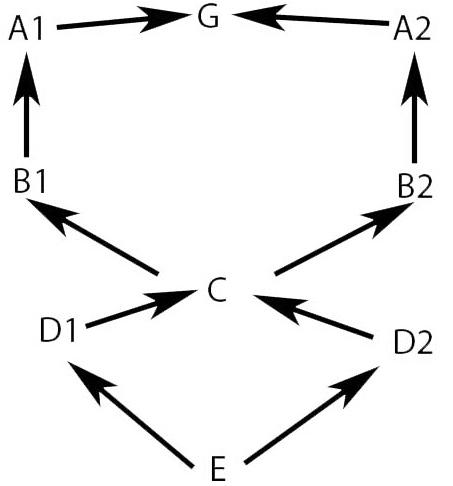
Здесь всё то же самое, только оканчивается на "G". При обходе будем иметь "E D2 C B2 A2 G B1 A1 G D1 C B2 A2 G B1 A1 G". В итоге, инвертировав, получим "G A1 B1 G A2 B2 C D1 G A1 B1 G A2 B2 C D2 E"
А что будет, допустим, если класс G унаследуют классы B1 и B2, причем B1 унаследует класс G после наследования класса A1, а B2 унаследует G до наследования A2. Все просто. Нам нужно будет писать "G" всякий раз, после того как мы обойдем ветвь "B2->A2->G".
Вот так все просто, когда у нас присутствует только лишь одно невиртуальное наследование. С виртуальным чуть сложнее, но ненамного.
Виртуальное наследование
Я буду обозначать виртуальное наследование красной стрелкой, а не виртуальное, как и раньше, черной.
Теперь у нас добавятся еще правила для обхода графа. Сразу обобщим на случай смешанного наследования, т.е. в котором есть как виртуальное, так и невиртуальное.
- Среди невиртуальных ветвей главнее та, что правее.
- Среди виртуальных ветвей главнее та, что правее.
- Невиртуальная ветвь главнее виртуальной.
- Класс наследуется только по одной виртуальной ветви, расположенной левее всех и по всем невиртуальным.
- При наличии невиртуальной альтернативы, обход графа временно прекращается по текущей ветви, если встретилась виртуальная. Обход продолжается после того, как будут недоступны невиртуальные альтернативы.
- При наличии виртуальных альтернатив, выбирается самая правая альтернатива, а по текущей ветви обход прерывается до тех пор, пока не будут исчерпаны все альтернативы, находящиеся правее.
Правила 5 и 6 на самом деле можно объединить в одно. Позже вы в этом убедитесь сами.
Думаю, вы поняли принципы построения графа в соответствии с листингами, и, так как связь между графом и листингом взаимно однозначная, далее я буду представлять только графы, чтобы не загромождать кодом статью.
Итак, рассмотрим первый пример.
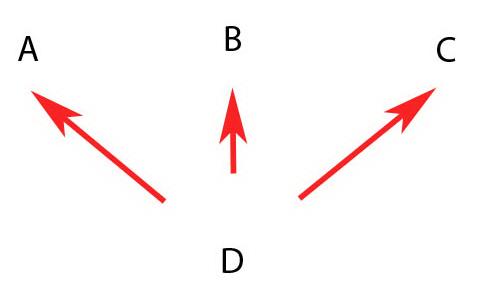
Здесь, как понятно из рисунка, "D" наследует виртуально три класса - "A", "B" и "C". Отлично! Применяем второе правило и получаем "D C B A", инвертируем - получаем "A B C D". Всё тривиально.
Рассмотрим немного иной пример.
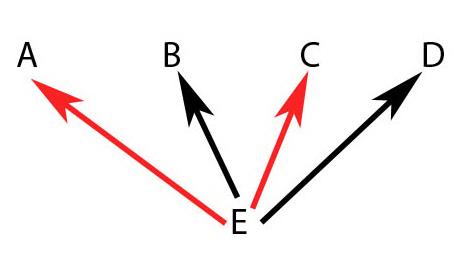
Видим, что у нас смешанное наследование. С чего начать? А об этом говорится в п.3 - начинаем с невиртуальных ветвей - "E D B", и заканчиваем на виртуальных - "C A". Отсюда, окончательно инвертировав, имеем "A C B D E".
А как будем поступать с этим?
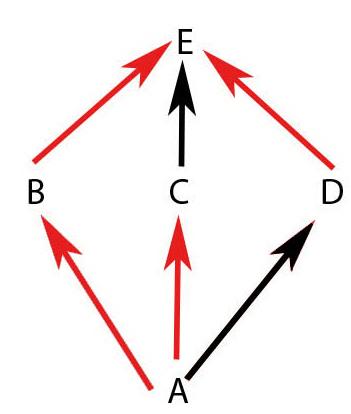
Да, действительно, сначала выбираем "AD" по п.3, но не торопитесь совершать переход по "DE", а лучше взгляните на п.4. Да, именно на п.4. Наследование будет проходить по пути "BE", и только по нему(!) среди виртуальных ветвей. Итак, мы имеем "AD", затем "CE", ведь невиртуальные ветви не влияют на виртуальные, а после - "BE". Инвертируя порядок, получаем "E B E C D A". Проще говоря, если мы видим, что к одному классу подходят несколько виртуальных ветвей, можем смело убирать все, кроме крайней левой.
В следующем примере нас ожидает одна тонкость.
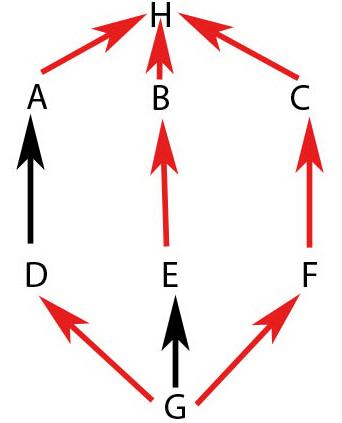
Начинаем как обычно с главной (в данном случае она единственная) невиртуальной ветви - "GE". Далее логично сделать переход на B, но нас должно насторожить то, что ветвь поменялась на виртуальную, а это значит, что следует "оглядеться" в поисках других невиртуальных ветвей (п.5) или виртуальных ветвей (п.6), которые могут иметь больший приоритет, чем текущая. И правда, такая есть, это - "GF", далее "C", и не забываем про п.4, поэтому "H" не включаем. Больше приоритетных альтернатив нет, поэтому продолжим обход - "EB", далее опять п.4, обход "GDAH". Если собрать все воедино, то получим следующий маршрут: "G E F C B D A H". Инвертируем: "H A D B C F E G"
Пример использования п.5 представлен ниже.
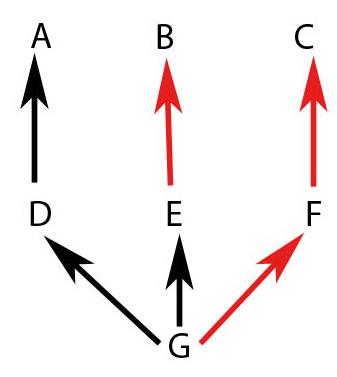
Начали - "GE", встретили виртуальную ветвь, нашли альтернативу "D", "A". Далее имеем еще одну виртуальную альтернативу (т.к. правее) "F", "G". Заканчиваем переходом на "B". Получаем "G E D A F C B". Итог - "B C F A D E G".
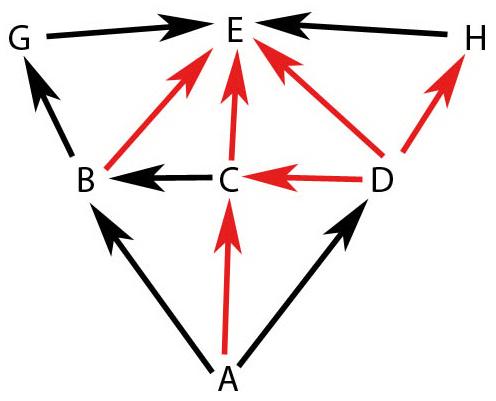
И, напоследок, рассмотрим такой экзотический пример. Согласно п.4, можно упростить граф, убрав ветви "DE", "CE" и "DC". Начинаем обход: "AD", встретив виртуальную ветвь после невиртуальной, ищем альтернативу: "BGE", возвращаемся к неоконченной ветви на "H", "E". Осталась виртуальная ветвь "AC", далее "B", "G", "E" и еще раз E по виртуальной ветви BE (действительно "E" может повторяться, ведь это не узел, в отличие от "G"). Имеем "A D B G E H E C B G E E". Инвертируя, получим "E E G B C E H E G B D A".
Итог
Вот мы и рассмотрели, пожалуй, все простые случаи и некоторые экзотические. Честно признаться, не знаю, где может применяться такое наследование, как в последнем примере, но, опять же, подчеркну академический характер задачи. Да и неплохо получить звание "Ходячий компилятор".