R - мощный функциональный язык программирования и среда анализа наборов статистических данных. Будучи средой анализа, R позволяет создавать различные графические представления данных из командной строки. Читайте первую часть этой серии статей и статью Камерона Лэйрда об R - из них можно больше узнать об R, о платформах, на которых может работать R, а также о наборе доступных для нее пакетов.
Как и интерактивные оболочки Python, Ruby, wish для Tcl/Tk и многие среды Lisp, оболочка R отлично подходит для исследования операций - использование редактируемых команд позволяет совершать различную обработку данных. В отличие от интерактивных оболочек многих других языков программирования, но в полном соответствии с ориентацией R на данные, оболочка R позволяет сохранять всю среду проекта (по одной на каждый рабочий каталог). Одна из полезных особенностей - история команд: ее можно просматривать, редактировать и сохранять в файле .Rhistory. Однако основная особенность сохранения среды рабочих проектов состоит в том, что все данные сохраняются в бинарной форме в файле .RData. Советуем регулярно использовать команду rm(), чтобы сохраняемая среда данных не разрасталась неограниченно (remove() - синоним для rm()).
Эта статья - вторая часть рассказа об R. Первая статья знакомит читателя с некоторыми базовыми типами данных R, включая векторы и многомерные массивы (2-мерные массивы еще называют матрицами), массивы данных для "умных" таблиц, списки для гетерогенных коллекций и т.д. В прошлой статье были также выполнены базовый статистический анализ и построение графиков для большого массива данных, собранного одним из соавторов (Брэдом): эти данные - годичная история изменения температуры вокруг дома Брэда, собранная с трехминутными интервалами времени. Подобно большинству реальных данных, эти температурные данные содержат дефекты и погрешности измерения - и в этой статье мы будем пытаться обнаружить подозрительные данные.
Наша статья решает две задачи. Во-первых, мы продолжим анализ данных, рассматривавшихся в предыдущей статье, чтобы подробнее рассмотреть возможности самого языка R. Во-вторых, мы исследует общие закономерности данных и покажем, как находить их, используя R.
R как язык программирования
Распространяемый по лицензии GPL язык программирования R имеет двух предков: S/S-PLUS и Scheme (Lisp). Особенно следует подчеркнуть связь со Scheme, так как основные особенности функционального программирования в R унаследованы от Scheme. Внимательные читатели могли отметить примечательное отсутствие в предыдущей статье одного существенного аспекта - управления выполнением программы! В этой статье мы по-прежнему не затрагиваем эту тему. На самом деле в R есть отличные команды if, else, while и for, очень похожие на аналогичные команды Python (в других языках синтаксис этих команд несколько другой). Плюс к тому есть еще и команды repeat, break, next и switch. Программисты, использующие процедурные языки, будут удивлены тем, насколько много можно сделать без управления выполнением - и еще больше они будут обескуражены, узнав, насколько проще становятся без этого многие задачи!
Объявляйте то, что вам нужно
Полностью в духе функционального программирования в R можно сделать практически все с помощью простых декларативных операторов. В R есть две особенности, которые в большинстве случаев делают управление выполнением излишним. Во-первых, вы уже видели, что большинство операций над объектами коллекций работают поэлементно. Чтобы сделать что-то над элементами вектора данных, не требуется цикл, так как можно просто выполнить операцию сразу со всеми элементами вектора:
Листинг 1. Поэлементные операции в R
> a = 1:10 # Диапазон значений от 1 до 10 > b = a+5 # Прибавление 5 к каждому элементу > b # Вывод вектора b [1] 6 7 8 9 10 11 12 13 14 15 |
Также можно оперировать только элементами с определенными индексами, используя "индексный массив":
Листинг 2. Использование индексных массивов для выбора элементов
> c = b # Копируем b в a > pos = c(1,2,3,5,7) # Изменяем первичные индексы > c[pos] = c[pos]*10 # Перераспределяем позиции индексов > c # Вывод вектора [1] 60 70 80 9 100 11 120 13 14 15 |
Или, что, возможно, лучше всего, можно использовать синтаксис, похожий на списочные выражения языков Haskell или Python, и оперировать только над элементами, имеющими требуемое свойство:
Листинг 3. Использование предикативного выбора элементов
> d = c > d[d %% 2 == 0] = -1 # Присваивание -1 всем четным элементам > d [1] -1 -1 -1 9 -1 11 -1 13 -1 15 |
Внимательные читатели могут заметить, что в этих примерах используется присваивание с помощью знака =, тогда как в большинстве примеров раньше использовались знаки <-. Знак равенства делает то же, что и стрелка, но может быть использован только в высокоуровневых операциях, но не в во вложенных выражениях. Если есть сомнения по поводу использования знака равенства, безопаснее использовать стрелку.
Анализируем данные о температуре
В первой статье мы с помощью функции read.table() считали примерно 170 тысяч показаний каждого из 4 датчиков. Однако для более удобного доступа к отдельным сериям измерений мы скопировали колонки данных в векторы, названные по местам размещения датчиков: outside (на улице), livingroom (гостиная), basement (подвал) и lab (лаборатория). Не нужно забывать, что некоторые результаты измерений были утеряны: иногда на записывающем компьютере происходили сбои, приборы иногда отказывали, не все 4 термометра были включены точно в один день и тому подобное. Другими словами, наши температурные данные во многом похожи на реальные данные, с которыми приходится иметь дело в жизни.
При первоначальном исследовании температурных данных была замечена аномалия в гистограммах. Она проявляется большим пиком наружной температуры вблизи 24 градусов Цельсия. Наше первое предположение заключалось в том, что эти пики отражают рассинхронизацию при записи, когда температура из внутреннего помещения записывалась в данные внешнего помещения (и, соответственно, наоборот). Чтобы проиллюстрировать возможности R, посмотрим, можно ли доказать или опровергнуть это предположение.
Поиск аномалий
Первый шаг в исследовании аномалий - это их нахождение. А именно, точечная аномалия должна характеризоваться большими скачками температуры с обеих сторон от точки данных. Еще конкретнее, мы можем ожидать, что 2 соседние с аномалией точки будут обычно намного выше или намного ниже, чем точка потенциальной аномалии. Например, простая последовательность температур (с трехминутным интервалом) "20, 16, 13" демонстрирует необычно быстрое падение температуры, но не порождает подозрения на одноточечную ошибку в среднем отсчете. Конечно, нельзя априори исключить существование других типов ошибок или погрешностей, затрагивающих не только единичные отсчеты данных.
Наши первые идеи по идентификации неправильных измерений были довольно сложны. Можно обратить внимание на высокочастотные компоненты преобразования Фурье наших последовательностей. Или можно взять производные векторов температуры (возможно, вторые производные, чтобы найти изгибы графика). Можно попытаться выполнить свертки температурных векторов. Все эти операции встроены в R. Но потом мы оставили высокие помыслы и спустились на землю. Мы ищем простую закономерность - это отсчеты температур, имеющие большие скалярные разности с соседними измерениями. Другими словами, нам достаточно простого вычитания.
Чтобы найти все разности между соседними точками данных, мы создадим таблицу данных, колонки которой будут соответствовать предыдущим, текущим и следующим точкам данных. Это позволит нам фильтровать всю таблицу данных, выбирая интересующие ряды.
Листинг 4. Поиск одиночных погрешностей в данных уличной температуры
> len <- length(outside) # Краткое имя длины вектора > i <- 1:(len-2) # Краткое имя вектора номеров строк колонок таблицы данных > # Создание таблицы данных для окна измерений на каждую строку > odf <- data.frame(lst=outside[1:(len-2)], + now=outside[2:(len-1)], + nxt=outside[3:len] ) > # Создание вектора локальных изменений температуры, добавление к таблице данных > odf$flux <- (odf[i,"now"]*2) - (odf[i,"lst"] + odf[i,"nxt"]) > odf2 <- odf[!is.na(odf$flux),] # Исключение "Not Available" измерений > oddities <- odf2[abs(odf2$flux) > 6,] # Странно, если отклонение больше 6 |
Итак, что мы имеем после фильтрации? Давайте посмотрим:
Листинг 5. Просмотр погрешностей в данных уличной температуры
> oddities
lst now nxt flux
2866 21.3 15.0 14.9 -6.2
79501 -1.5 -6.2 -4.1 -6.8
117050 21.2 24.6 21.6 6.4
117059 20.6 23.4 20.1 6.1
127669 24.1 21.2 24.7 -6.4
127670 21.2 24.7 21.5 6.7
|
Эти данные говорят о том, что имеются точки с сильным отличием относительно соседних измерений. Но большая часть из них не выглядит как кандидаты на ошибки синхронизации. Например, в интервале времени 79501 температура 6.2 окружена двумя явно более высокими температурами. Однако ни одна из них не выглядит похожей на температуру внутри дома, скорее уж это очень холодный порыв ветра.
С другой стороны, похоже, что мы имеем перестановки около временных интервалов 117059 и 12670. Средние значения температур близки к внутренней (24 градуса), а соседние измерения значительно ниже - хотя это и не мороз. Может быть, это измерения, сделанные весной.
Оформление полезных операций в функцию
Теперь нам нужно узнать, имеют ли наши кандидаты на перестановку соответствия в других отсчетах. Если мы найдем подходящие данные уличной температуры в одном из наборов данных температур внутри дома, это подтвердит нашу гипотезу. Но мы не хотим заново набирать программу, меняя везде outside на lab. Что действительно стоит сделать - это объединить всю последовательность операций в одну функцию:
Листинг 6. Оформление процесса обнаружения отклонений в функцию
oddities <- function(temps, flux) {
len <- length(temps)
i <- 1:(len-2)
df <- data.frame(lst=temps[1:(len-2)],
now=temps[2:(len-1)],
nxt=temps[3:len])
df$flux <- (df[i,"now"]*2) - (df[i,"lst"] + df[i,"nxt"])
df2 <- df[!is.na(df$flux),]
oddities <- df2[abs(df2$flux) > flux,]
return(oddities)
}
|
Имея функцию, значительно проще обрабатывать различные наборы данных и устанавливать пороги отклонений. Запуск функции oddities(lab,6)не выдает отметок времени наших кандидатов на перестановку (равно как и для livingroom и basement). Однако взгляд на записи температур лаборатории преподносит другой сюрприз:
Листинг 7. Огромные температурные колебания в лаборатории
> oddities(lab, 30)
lst now nxt flux
47063 19.9 -2.6 19.5 -44.6
47268 17.7 -2.6 18.2 -41.1
84847 17.1 -0.1 17.0 -34.3
86282 14.9 -1.0 14.8 -31.7
93307 14.2 -6.4 14.1 -41.1
|
Показаний такого сорта мы не ожидали. Может быть, лучшее объяснение - это то, что Брэд открывал окно лаборатории в жестокий мороз. Если так, то Дэвид поражается эффективности камина Брэда, восстанавливающего тепло всего за 3 минуты вентиляции комнаты.
Правильное объяснение
Возможно, просмотр полных данных по интересующим нас моментам времени разъяснит ситуацию:
Листинг 8. Полный набор записей температур вблизи шага 47063
> glarp[47062:47066,]
timestamp basement lab livingroom outside
47062 2003-10-31T17:07 21.5 20.3 21.8 -2.8
47063 2003-10-31T17:10 21.3 19.9 21.2 -2.7
47064 2003-10-31T17:13 20.9 -2.6 20.9 -2.6
47065 2003-10-31T17:16 20.8 19.5 20.8 -2.6
47066 2003-10-31T17:19 20.5 19.4 20.7 -2.8
|
Во-первых, заметим, что отметки времени, возвращаемые функцией oddities(), завышены на единицу. Ах да, мы использовали смещение для создания окна для каждой строки таблицы данных. При этом, вся совокупность данных говорит в пользу идеи "открытых дверей" - накануне Хэллоуина в 5 часов вечера в Колорадо может быть весьма прохладно, а температура может сильно меняться, когда в двери Брэда заглядывают гуляющие (и получают свои конфеты за 3 минуты). Итак, возможно, эта загадка разрешена.
И все-таки, что же насчет загадки, начавшей наши исследования? Почему появляются пики около 24 градусов в измерении уличной температуры? Может быть, необходимо посмотреть на гистограмму более внимательно? В частности, можно использовать предикативный критерий для индексирования вектора и сузить гистограмму до интересующего нас температурного диапазона:
Листинг 9. Сужение температурного диапазона
hist(outside[outside < 26 & outside > 23],
breaks=90, col="green" border="blue")
|
Рисунок 1. Гистограмма для улицы в суженной температурной области 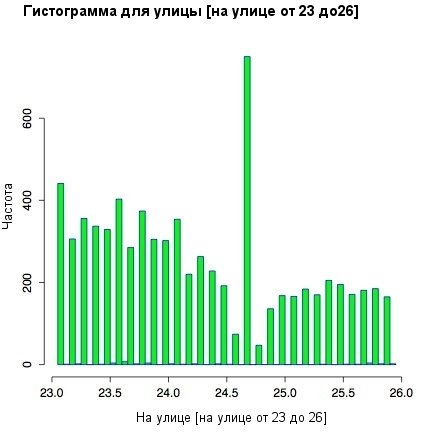
Посмотрев подробнее на локализованные температурные пики, можно обнаружить отдельные впадины справа от каждого пика. Они видны, если посмотреть на отклонения в десятые доли для промежутка рядом со значением 24.7 градуса. Наиболее вероятно, что это является следствием погрешности округления термометра. Отлично, но все же мы еще не уверены. Даже после некоторого сглаживания небольшой пик все-таки остается.
Промежуточный статистический анализ
Одна из сильных сторон R - это способность рассчитывать линейные и нелинейные модели регрессий. Рассмотрим простой пример. Создадим два вектора: x будет временем в днях, начиная с даты начала сбора данных, а y будет соответствующей температурой на улице.
Листинг 10. Создание вектора регрессии
> y <- glarp$outside > x <- 1:length(y)/(24*60/3) |
Можно подобрать прямую для этих значений:
Листинг 11. Подбор линейной регрессии
> l1 = lm(y ~ x)
> summary(l1)
Call:
lm(formula = y ~ x)
Residuals:
Min 1Q Median 3Q Max
-29.4402 -7.4330 0.2871 7.4971 23.1355
Coefficients:
Estimate Std. Error t value Pr(>/t/)
(Intercept) 10.2511014 0.0447748 228.95 <2e-16 ***
x -0.0037324 0.0002172 -17.19 <2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 9.236 on 169489 degrees of freedom
Multiple R-Squared: 0.00174, Adjusted R-squared: 0.001734
F-statistic: 295.4 on 1 and 169489 DF, p-value: < 2.2e-16
|
Знак "~" означает формулу. Это действие указывает R найти коэффициенты A и B, которые минимизируют формулу sum((y[i]-(A*x[i]+B))^2). Лучшие значения - когда A равно -0.0037324 (очень близкий к нулю угол), а B равно 10.2511014. Заметим, что остаточная стандартная погрешность равна 9.236, что мало отличается от стандартного отклонения самого y. Это говорит о том, что простая линейная функция от времени - очень плохая модель для анализа уличной температуры.
Возможно, лучше было бы использовать аппроксимацию синусами и косинусами с периодами 1 день и 1 год. Такую модель можно попробовать, изменив формулу на следующую:
Листинг 12. Попытка приближения тригонометрическими кривыми
> l2 = lm(y ~ +I(sin(2*pi*x/365)) +I(cos(2*pi*x/365)) + +I(sin(2*pi*x)) +I(cos(2*pi*x)) ) |
Синтаксис этой формулы очень хитер: внутри вызовов I() арифметические функции имеют свое обычное назначение. Например, в первый вызов I() записано следующее выражение: 2 умножить на pi, умножить на x и делить на 365. Знак "+" перед I() указывает не на сложение, а на то, что выражение после + должно быть включено в модель. Результат может быть отображен, как обычно, с помощью команды summary().
Листинг 13. Результаты тригонометрической регрессии
> summary(l2)
Call:
lm(formula = y ~ +I(sin(2 * pi * x/365)) +I(cos(2 * pi * x/365))
+I(sin(2 * pi * x)) +I(cos(2 * pi * x)))
Residuals:
Min 1Q Median 3Q Max
-21.7522 -3.4440 0.1651 3.7004 17.0517
Coefficients:
Estimate Std. Error t value Pr(>/t/)
(Intercept) 9.76817 0.01306 747.66 <2e-16 ***
I(sin(2 * pi * x/365)) -1.17171 0.01827 -64.13 <2e-16 ***
I(cos(2 * pi * x/365)) 10.04347 0.01869 537.46 <2e-16 ***
I(sin(2 * pi * x)) -0.58321 0.01846 -31.59 <2e-16 ***
I(cos(2 * pi * x)) 3.64653 0.01848 197.30 <2e-16 ***
---
Signif. codes: 0 `***' 0.001 `**' 0.01 `*' 0.05 `.' 0.1 ` ' 1
Residual standard error: 5.377 on 169486 degrees of freedom
Multiple R-Squared: 0.6617, Adjusted R-squared: 0.6617
F-statistic: 8.286e+04 on 4 and 169486 DF, p-value: < 2.2e-16
|
Остаточная ошибка все еще велика (5.377), но утешим себя тем фактом, что погода в Колорадо исключительно непредсказуема.
R предоставляет множество инструментов для анализа временных данных. Например, мы можем построить график функции автокорреляции для температуры в гостиной:
Листинг 14. Функция автокорреляции температуры в гостиной
> acf(ts(glarp$livingroom, frequency=(24*60/3)), + na.action=na.pass, lag.max=9*(24*60/3)) |
Рисунок 2. График функции автокорелляции температуры в гостиной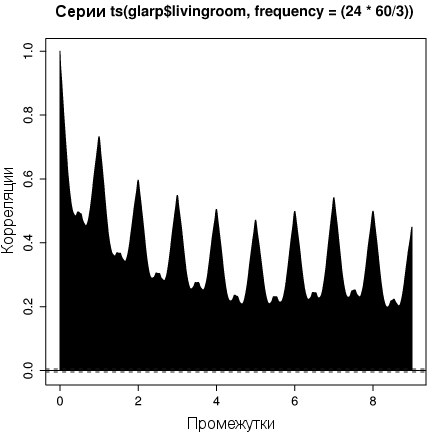
Встроенная функция ts() создает временной ряд из вектора glarp$livingroom. Частота выборки задается в отсчетах в день. Неудивительно, что температура сильно коррелирует, когда сдвиг составляет целое количество дней. Заметны также небольшие пики на семи днях. Причина этого в том, что термостат Брэда устанавливает другую температуру на выходных (когда Брэд обычно уходит из дома на весь день), в результате, корреляции при установке семидневного окна оказываются чуть больше.
Заключение
Итак, мы использовали R для анализа структуры и аномалий в наборах данных, которые имеют точно такие же недостатки и потенциальные проблемы, как и практически все реальные научные данные. В этой статье мы также увидели, как стиль функционального программирования, реализованный в R, помогает быстро исследовать закономерности, данные и аналитические сценарии. В третьей части этой серии мы продолжим поиск закономерностей в больших наборах данных, используя более сложные статистические методы (но все равно затрагивая лишь малую часть богатейших возможностей R).
