 (13)
(13)| СТАТЬЯ |
27.03.02
|
Как создать корпоративную автоматизированную систему для расчета прозрачных плановых затрат (Часть 2)
©
К. Шлемензон ,
к.ф.-м.н., доцент СГУПС
Соотношения для расчета объемов. Заметим, что не для всех видов продукций понятие объема имеет смысл, и не для всех продукций объемы надо рассчитывать. Для некоторых из них объемы задаются заранее. Рассчитывать же надо лишь веса (объемы) тех дуг, которые нормируются и, возможно, те, которые присутствуют в таблице 10. Рассмотрим пример. Пусть одна и та же продукция изготавливается разными технологическими процессами, затем она "перемешивается" и используется как усредненная. Усредненная продукция может нормироваться, следовательно, ее объем рассчитывается. Поэтому, каким-либо способом должен рассчитываться объем каждой из объединяемых продукций. Один из вариантов заключается в том, чтобы объемы некоторых из объединяемых продукций задавать заранее, а объемы остальных задавать по пропорциям от объема суммируемой продукции. Математически это выражается следующим образом:
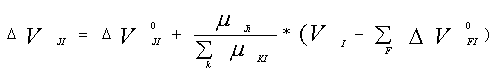 (13)
(13)
Здесь ![]() - величина заранее заданного объема - берется из колонки 4 таблицы 10 (при ненулевом
заданном объеме величина
- величина заранее заданного объема - берется из колонки 4 таблицы 10 (при ненулевом
заданном объеме величина ![]() =
0). Коэффициент
=
0). Коэффициент![]() берется из колонки 3. Множество K есть набор номеров узлов, являющихся началом
для входящих в узел J дуг, для которых
берется из колонки 3. Множество K есть набор номеров узлов, являющихся началом
для входящих в узел J дуг, для которых ![]() =0,
F есть набор номеров узлов, являющихся началом для входящих в узел J дуг, для
которых
=0,
F есть набор номеров узлов, являющихся началом для входящих в узел J дуг, для
которых ![]() #
0.
#
0.
Соотношения для себестоимостей. В практике ненормативного способа распределения затрат одной продукции на несколько используют пропорции. В качестве коэффициентов пропорциональности на некоторых предприятиях берут фонд зарплаты, на других - объемы производств, на третьих - объемы уточняют эмпирическими коэффициентами (сложности). Главное, что все эти коэффициенты от самих себестоимостей не зависят.
Все вышеописанные способы описываются обобщающей формулой, которая, как частный случай, содержит способ распределния затрат пропорцианольно зарплате, либо объемам производства продукций
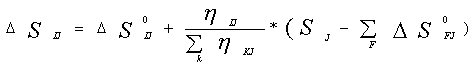 (14)
(14)
Здесь ![]() - величина заранее заданных затрат в рублях - колонка 4 таблицы 9 - (при ненулевых
заданных затратах величина
- величина заранее заданных затрат в рублях - колонка 4 таблицы 9 - (при ненулевых
заданных затратах величина ![]() =
0). Коэффициент
=
0). Коэффициент ![]() берется
из колонки 3 таблицы 9. Множество K есть набор номеров узлов, являющихся концом
для исходящих из узла J дуг, для которых
берется
из колонки 3 таблицы 9. Множество K есть набор номеров узлов, являющихся концом
для исходящих из узла J дуг, для которых ![]() =
0, F есть набор номеров узлов, являющихся концом для исходящих из узла J дуг,
для которых
=
0, F есть набор номеров узлов, являющихся концом для исходящих из узла J дуг,
для которых ![]() #
0.
#
0.
Набор формул (10)- (14) фактически завершает разработку математической модели для расчета плановых затрат. Если задать начальные значения объемов товарной продукции и всех коэффициентов, участвующих в формуле (11) и (13) то этого достаточно, чтобы рассчитать все неизвестные объемы. Рассмотрим для простоты случай, когда граф не содержит циклов и петель. Узлы (вершины), не имеющие исходящих ребер назовем товаром (Т - это последний этап переработки продукций), а узлы без входящих дуг назовем ресурсами (Р - на них нет калькуляций).
Разобьем узлы на уровни. К уровню 0 отнесем узлы товар. Для этого уровня объемы заданы. Условно отбросим все ребра, входящие в узлы уровня 0. Их вес (объем) рассчитывается на основе весов узлов - товара. Отнесем к уровню 1 узлы, которые в новом графе не будут иметь исходящих дуг. Из этих узлов могли исходить только отброшенные дуги. Следовательно, вес узлов уровня 1 также рассчитывается, как сумма известных весов исходящих дуг. Далее, по индукции, доказываем, что можно рассчитать веса всех узлов.
Таким образом, задав план производства товарной продукции, мы могли бы рассчитать все объемы калькуляций, включая ресурсы. К ресурсам обычно относится покупная продукция, либо условно- постоянные затраты. Для тех и других можно определить значения полных затрат. Для покупных материалов известна цена за единицу продукции, умножив ее на рассчитанный полный объем, получаем полные затраты. Условно - постоянные затраты (деньги) известны до начала расчетов.
Предположим теперь, что мы знаем объемы всех калькуляции и полные затраты ресурсов. Тогда, повторяя почти дословно рассуждения об уровнях, но, уже двигаясь от узлов ресурсов в направлении к товару, имеем возможность расчета себестоимостей всех узлов.
Если в графе есть циклы и петли (например, наличие возвратных отходов), тогда необходимо решать связанную систему линейных алгебраических уравнений, для которой все коэффициенты известны.
Сами по себе соотношения (10) - (14) для экономистов- практиков большой пользы не представляют. Пока неясно, как реально, на основе привычной для них информации сконструировать уравненияiii.
Практический алгоритм построения математической модели. Исходим из реальной ситуации, что потенциальный пользователь АС не владеет не только терминами теории графов, но высшей математикой вообще. Однако он хорошо знает производство и методику калькулирования плановых затрат. На первом этапе предложим экономистам все свои калькуляции привести к единой формеiv:
Плановая калькуляция (на продукцию)
Таблица 11
|
Наименование позиции |
На весь объем производства |
На единицу объема производства
|
|||
|
Количество |
Цена |
Сумма |
Норма
|
Сумма
|
|
|
1
|
2
|
3
|
4
|
5
|
6
|
Эта работа по систематизации данных заставит экономистов выделить все виды продукции, которые калькулируются. Обычно обнаруживается, что экономист обрабатывает значительно больше калькуляций, чем ему казалось. Далее, необходимо каждому пользователю выделить "вилку номеров" (например, от 1201 до 1300) и предложить, в рамках "вилки", произвольным образом закодировать свои калькуляции. Программистам нужно разработать две таблицы, назовем их Kalk и Pozic, и поместить на сервере. В первой, открытой полностью для всех таблице, должны быть список заголовков калькуляций, во второй - список всех позиций. Между таблицами должна быть реляционная связь "один ко многим". Во второй таблице каждый пользователь должен иметь доступ только к своей "вилке" номеров. Затем нужно взять готовые калькуляции какого - либо прошедшего временного периода и попросить пользователей ввести их в ПЭВМ через интерфейс, разработанный программистами.
Этим мы фактически сконструировали узлы графа будущей модели (номера калькуляций) и определили количество дуг (число позиций). Дальнейшая работа заключается в том, чтобы "привязать" начало дуг к узлам. Концы дуг привязаны - это номера калькуляций, в которых они присутствуют в качестве затрат.
Надо заметить, что, введя описанным образом информацию, мы уже построили модель, позволяющую решать задачу планирования. Модель представляет собой многокомпонентный граф. Для каждого пользователя все затраты являются ресурсами, стоимости которых надо знать заранее, а его продукция является товаром, объем производства которого надо задать.
Будем улучшать модель следующим образом. Необходимо ввести в таблицу Pozic необходимое число дополнительных полей, которые бы позволили однозначно определить узел, откуда выходит дуга - позиция. Можно рекомендовать следующий перечень из 9 полей (таблица 12)
Таблица 12
|
I |
J |
NIJ |
S0IJ |
|
V0IJ |
|
Kodc |
Proch |
|
1 |
2 |
3 |
4
|
5 |
6 |
7 |
8 |
9 |
Комментария требуют лишь некоторые поля. Поле 2 будет соответствовать номеру калькуляции (ссылка), которая используется в качестве статьи затрат. В этом случае цена (колонка 3 табл.11) определяется значением себестоимости калькуляции, на которую ссылка. Поле Kodc - соответствие коду из справочника покупной продукции. Цена передается из этого справочника. Поле 9 соответствует кодам некоторого справочника прочих затрат, в который включается, например, амортизация, налоги и т.д. Каждому пользователю предлагается проанализировать статьи затрат своих калькуляций и связать их с одним из отмеченных справочников, путем выбора кода.
Далее, нужно разобраться с делимыми и суммируемыми калькуляциями. Рекомендуется вводить их в таблицы типа 9 и 10, а путем пересчета наполнять поля в таблице 12.
Заметим, что процесс "улучшения модели" может протекать непрерывно, но методика расчета себестоимости будет работать. Единственно, потребуется изменять граничные условия, то есть некоторые объемы и затраты надо будет задавать как исходные. Причем, как будет показано ниже, имеется возможность наглядно показать, что надо задавать. У начальника ПЭС появляется возможность проводить эксперименты над методикой расчета себестоимости, изменяя способы преобразования затрат.
После того, как данные таблицы 12 будут заполнены, коэффициенты модели можно построить следующим образом.
Алгоритм для расчета объема.
Перепишем систему уравнений (10) в виде
![]() (16)
(16)
Конкретные выражения коэффициентов явно использоваться не будут, поэтому здесь не расписываютсяv. Если подставить (16) в (17), то получим замкнутую систему линейных алгебраических уравнений с неоднородной правой частью.
Выполним следующие действия:
Шаг 1. Среди полного списка калькуляций выделим те, объемы которых надо рассчитать. Это калькуляции, на которые есть ссылки и объединяемые калькуляции. Выделим эти записи красным цветом. Остальные - другим цветом. Объемы последнихvi должны быть заданы до начала счета.
Шаг 2. Поместим номера с красным цветом в одномерный массив
A. Пусть N - длина массива. Введем двумерный массив D размерности Nx(N+1) -
расширенную матрицыvii системы линейных алгебраических уравнений
относительно неизвестных объемов. Поместим значение 0 во все элементы D, затем
проставим - 1 по диагонали матрицы, то есть ![]()
Шаг 3. В цикле I от 1 до N перебираем содержимое массива
A. Для каждого элемента А перебираем все записи таблицы Pozic, соответствующие
калькуляции с номером элемента массива. Проводим анализ значений полей, описанных
в таблицы 12. Определяем номер калькуляции, которая является узлом для входа
позиции - ребра. Через массив A пытаемся определить этот номер в списке элементов.
Здесь возможны ситуации - номер присутствует среди элементов A и номер отсутствует.
Если номер отсутствует, значит, объем калькуляции ему соответствующий, задается
заранее. Следовательно, левая часть формулы (16) есть константа ![]() Поэтому корректируем матрицу D следующим образом:
Поэтому корректируем матрицу D следующим образом:
![]() (17)
(17)
Допустим теперь, что номер в списке найден и соответствует элементу J. В этом случае должна иметь место формула (15). Корректируем D следующим образом:
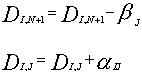
В результате будут получены числовые значения коэффициентов матрицы D.
Шаг 4. Численным методом решаем полученную систему линейных алгебраических уравнений и определяем неизвестные объемы.
Алгоритм для расчета себестоимостей принципиально ни чем не отличается от алгоритма для объемов. При этом объемы должны быть уже рассчитаны.
Рассмотрим, какие основные выходные документы можно получить в рамках данных моделей (информационной и математической).
Во-первых, все калькуляция с любой глубиной приложения развернутых цифрviii. Под этим и понимается прозрачность затрат. Во-вторых, всевозможные сводные сметы (калькуляции). Для этого достаточно "сконструировать" соответствующую суммируемую калькуляцию. В-третьих, так называемую "шахматку" по затратам каждого подразделения в разрезе статей затрат (колонки 6 таблицы 8). В-четвертых, потребные ресурсы покупных материалов. В-пятых, в рамках данной модели можно, в качестве покупной продукции ввести "человеко-часы" и рассчитать трудоемкость изготовления продукции. Если задать рыночные цены товарной продукции, то можно оценить ожидаемую прибыль предприятия.
Это лишь часть документов, которые можно получить в рамках данной модели. Использование техники запросов к реляционной базе данных позволяет конструировать новые выходные документы.
В заключение, в качестве приложения теории графов, рассмотрим задачу (в упрощенном варианте) о расчете себестоимости продукции в прямых затратах. Представить калькуляцию в прямых затратах это значит выразить ее себестоимость в виде суммы затрат, каждая из которых представляет собой ресурс.
Будем считать что, модель производства представляет собой связанный
граф, без циклов и петель. Рассмотрим две произвольных вершины i, j соединенных
ребром от i к j. Пусть вес ребра будет определяться либо формулой (11), либо
упрощенным вариантом формулы (13):
![]() (18)
(18)
В (11) доля объема рассчитывается через объем узла инцидентного
концу ребра, а в (18) через объем инцидентного началу ребра. Заметим, что если
положить 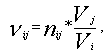 то формула (18) примет вид, аналогичный (11). Поэтому, мы можем ограничиться
рассмотрением случая только нормированного способа распределения затрат (формула
(11)).
то формула (18) примет вид, аналогичный (11). Поэтому, мы можем ограничиться
рассмотрением случая только нормированного способа распределения затрат (формула
(11)).
Рассмотрим два произвольных узла ![]() и
и ![]() . Определим,
какой объем продукции
. Определим,
какой объем продукции ![]() используется для производства продукции
используется для производства продукции ![]() .
Для этого выделим любую последовательность ребер, представляющую собой путь
(цепь), связывающую начальный и конечный узел.
.
Для этого выделим любую последовательность ребер, представляющую собой путь
(цепь), связывающую начальный и конечный узел.
Приведем следующую теорему.
Теорема.
Если веса всех ребер пути рассчитываются по нормированному закону (11),
то
![]() (19)
(19)
если же они все рассчитываются по ненормированному закону (18), то
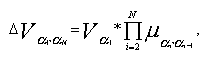 (20)
(20) если же они все рассчитываются по ненормированному закону (18), то
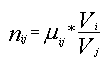 (21)
(21) Для того чтобы посчитать долю одной продукции в другой надо просуммировать левые части соотношений (19) - (20) по всем возможным связывающих их путям.
Доказательство. Теорема доказывается методом математической индукции. Рассмотрим прежде случай, когда N=1, то есть все пути имеют единичную длину. Это соответствует связи двух узлов несколькими параллельными дугами, что эквивалентно одной дуге с суммарной нормой. Поэтому, для этого случая утверждение имеет место.
Допустим, что утверждение имеет место для случая, когда длина путей не превосходит N-1 и докажем, что это же будет верно для путей длины N.
Рассмотрим рис. 2.
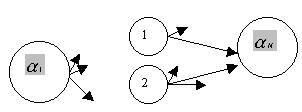
Рис. 2
Пусть в узел ![]() входят дуги, исходящие из узлов 1, 2, …. В свою очередь узлы 1, 2, … связывают
с узлом
входят дуги, исходящие из узлов 1, 2, …. В свою очередь узлы 1, 2, … связывают
с узлом ![]() пути длиной не более N-1. Согласно (18)
пути длиной не более N-1. Согласно (18)
![]() (22)
(22)
По предположению, в узле 1 содержится объем узла ![]() ,
рассчитываемого для каждого из путей по формуле (20). Поэтому для определения
доли объема
,
рассчитываемого для каждого из путей по формуле (20). Поэтому для определения
доли объема ![]() в узле 3 нужно, согласно (22), долю в узле 1 умножить на коэффициент распределения,
проделать это для узла 2 и для всех остальных узлов (если такие имеются),
соединенных через ребро с узлом 3. Но это приведет лишь к тому, что структура
формулы (для каждого пути) не изменится. Надо лишь в значении конечного индекса
N-1 заменить на N. Теорема доказана.
в узле 3 нужно, согласно (22), долю в узле 1 умножить на коэффициент распределения,
проделать это для узла 2 и для всех остальных узлов (если такие имеются),
соединенных через ребро с узлом 3. Но это приведет лишь к тому, что структура
формулы (для каждого пути) не изменится. Надо лишь в значении конечного индекса
N-1 заменить на N. Теорема доказана.
Эта теорема указывает принципиальные пути решения задачи о расчете себестоимости любой продукции в прямых затратах. Для этого надо выделить все пути, соединяющие соответствующую пару узлов и воспользоваться соотношениями (19) - (21). Задача определения всех путей в теории графов достаточно исследована [9].
Литература
Дополнительную информацию Вы можете получить в компании Interface Ltd.
Обсудить на специализированном
форуме по ERP-системам
Отправить
ссылку на страницу по e-mail
| Interface Ltd. Отправить E-Mail http://www.interface.ru |
|
| Ваши
замечания и предложения отправляйте
автору По техническим вопросам обращайтесь к вебмастеру Документ опубликован:27.03.02 |