| СТАТЬЯ |
22.03.02
|
©
К. Шлемензон ,
к.ф.-м.н., доцент СГУПС
Для крупного предприятия планирование деятельности обычно заключается не в использовании методов оптимизации, а в вариантных расчетах с оценкой ожидаемой себестоимости и прибыли по товарной продукции. В процесс калькулирования задействовано много людей, каждый из которых решает свои локальные задачи. Они вынуждены обмениваться информацией друг с другом. Не редки ситуации, когда один работник изменил свои цифры, а другой перенос данных и пересчет не выполнил. Уследить за этим очень трудно. Наличие компьютерной сети частично облегчает работу по передаче данных, но принципиально проблему не решает. Степень достоверности конечных плановых цифр не всегда на высоте. Большим желанием начальника ПЭС является автоматизация пересчета плана загрузки предприятия без привлечения множества работников. В идеале хотелось бы, чтобы основная масса экономистов, связанная с калькулированием продукции, собирала и вводила в ПЭВМ первичную информацию, а все вариантные расчеты выполнял один человек, например, сам начальник ПЭС.
На большинстве крупных предприятий существуют конкретные методики планирования - калькулирования затрат, которые обычно сопровождают работники - практики, знающие реальное производство, но не владеющие методами математического моделирования. В отдельных своих разделах система планирования не подчиняется строгим логическим закономерностям. Поэтому автоматизация ПЭС намного слабее всех других систем документооборота.
Выход может быть в том, что бы предложить экономистам автоматизированную систему (АС), позволяющую, во-первых, работать именно с той методикой планирования, которая принята на предприятии даже в чем-то и противоречивая. При этом необходимо показать, в чем заключаются противоречия, например, дисбаланс расходов. Только в этом случае можно запустить систему в эксплуатацию и сопоставить цифры. Кроме того, АС должна позволять при минимальных затратах труда улучшать методику планирования, ликвидируя различные дисбалансы и другие некорректности.
Ниже, на основе обобщения практического опыта автора по разработке программных
комплексов для нескольких крупных градообразующих предприятий, предложена модель
такого типа. Данная статья является развитием работ [1 - 6].
Предлагается описывать модель предприятия для расчета плановых затрат как процесс
постепенного усложнения более простых моделей.
Рассмотрим предприятие как объединение структурных подразделений, каждое из которых выпускает одно- номенклатурную продукцию. Благодаря последнему допущению для каждого подразделения имеет смысл понятие объема производства.
Рассмотрим следующую таблицу под названием СМЕТА.
Таблица 1
|
Кому |
Кто |
Сумма |
|
1 |
2 |
3 |
Здесь колонки 1 и 2 соответствуют условным кодам подразделений, колонка 3 - деньги. Смысловое содержание каждой строки таблицы следующее: подразделение с кодом "кто" оказывает услугу подразделению "кому" на величину "сумма". Для каждого подразделения предусмотрим еще наличие строчек, у которых (для условности) значение поля "Кто" равно нулю, а величина "Сумма" равна затратам подразделения, не связанных с услугами от других подразделений.
Представим себе следующую ситуацию. Мы создали компьютерную сеть звездной архитектуры, поместили базу данных со структурой таблицы 1 на сервер, закодировали подразделения и предложили экономистам предприятия ввести информацию в таблицу 1 о своих подразделениях. Заметим, что так представленная информация является полной и не избыточной. В таблице отсутствуют записи (затраты), которые являются производными от уже введенных затрат. Обрабатывая эту таблицу, мы смогли бы получить много аналитической экономической информации.
Во-первых, полные затраты предприятия. Для этого достаточно просуммировать
колонку 3 для тех записей, у которых "Кто" нуль (об этом будет сказано
далее). Во- вторых, структуру затрат каждого подразделения ![]() - его смету. Для этого надо выделить записи по условию "кому" =
- его смету. Для этого надо выделить записи по условию "кому" = ![]() .
В-третьих, можно определить полные затраты каждого подразделения, а разделив
их на объем - получить себестоимость единицы продукции.
.
В-третьих, можно определить полные затраты каждого подразделения, а разделив
их на объем - получить себестоимость единицы продукции.
Обобщим таблицу, предположив, что одно подразделение оказывает другому подразделению услугу не в рублях, а в объемах. Сумму надо рассчитать. Для этого введем две новые колонки "количество" и "цена":
Таблица 2
|
Кто |
Кому |
Количество |
Цена |
Сумма |
|
1 |
2 |
3 |
4 |
5 |
Имеет место
![]() (1)
(1)
для записей, где "Кто" не равно 0.
Для "Кто" = 0 можно записать
![]() (2)
(2)
( ![]() -
не зависящая от
-
не зависящая от![]() постоянная, сомножитель
постоянная, сомножитель ![]() введен для удобства)
введен для удобства)
![]() (3)
(3)
Здесь K с индексом означает содержимое соответствующей колонки, Vp - объем производства продукции подразделением P. Формула (3) показывает, что для расчета цены (себестоимости единицы) продукции подразделения P нужно прежде определить полные затраты этого подразделения (сумма в скобках) затем разделить на объем производства.
Уравнение (3) представляет собой систему линейных алгебраических уравнений относительно неизвестных цен продукций с неоднородной правой частью. Порядок уравнений равен числу анализируемых подразделений. В расписанном виде они совпадают с известными уравнениями баланса услуг вспомогательных подразделений [7]. Балансовые модели Леонтьева имеют такую же структуру [8]. Решение этих уравнений позволяет получить согласованную со всеми себестоимость каждой продукции. Для иллюстрации рассмотрим модельную задачу.
При этом не будем обращать внимания на единицы размерности. Предположим, что существуют нормы расхода, по которым одно подразделение оказывает услуги другому.
Пусть на предприятии существует всего два подразделения - гараж
и прачечная. Представим их сметы затрат следующими таблицами:
Смета для прачечной (Объем производства V = 100)
Таблица 3
|
Статья затрат |
Норма |
На объем |
Цена |
Затраты на весь объем |
|
Услуги гаража
|
0,5
|
50
|
|
|
|
Зарплата основных рабочих
|
1
|
100
|
20
|
2000
|
|
Амортизация
|
|
|
|
500
|
Смета для гаража (Объем производства V = 300)
Таблица 4
|
Статья затрат |
Норма |
На объем |
Цена |
Затраты на весь объем |
|
Услуги прачечной
|
0,3
|
90
|
|
|
|
Зарплата основных рабочих
|
0,8
|
240
|
20
|
4800
|
|
Амортизация
|
|
|
|
600
|
|
Итого
|
||||
Таблица 2 для данного случая примет вид:
Таблица 5
|
Кто |
Кому |
Количество |
Цена |
Сумма
|
|
2 |
1 |
50 |
|
|
|
0 |
1 |
|
|
2000 |
|
0 |
1 |
|
|
500 |
|
1 |
2 |
90 |
|
|
|
0 |
1 |
|
|
4800 |
|
0 |
|
|
|
600 |
Система уравнений экономического баланса затрат (3) примет следующий вид i
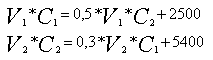
(Здесь![]() - неизвестные себестоимости и известные объемы услуг прачечной и гаража, соответственно).
Решение последней системы уравнений дает
- неизвестные себестоимости и известные объемы услуг прачечной и гаража, соответственно).
Решение последней системы уравнений дает
C1 = 40, C2 = 30.
Теперь мы можем заполнить все колонки таблиц 1 и 2:
Смета для прачечной (Объем производства V = 100)
Таблица 6
|
Статья затрат |
Норма |
На объем |
Цена |
Затраты на весь объем |
|
Услуги гаража |
0,5 |
50 |
30
|
1500 |
|
Зарплата основных рабочих |
1 |
100 |
20 |
2000 |
|
Амортизация |
|
|
|
500 |
|
Итого |
|
|
|
4000 |
Себестоимость единицы услуг прачечной C1= 4000/100 = 40
Смета для гаража (Объем производства V = 300)
Таблица 7
|
Статья затрат |
Норма |
На объем |
Цена |
Затраты на весь объем |
|
Услуги прачечной |
0,5 |
90 |
40
|
3600 |
|
Зарплата основных рабочих |
1 |
240 |
20 |
4800 |
|
Амортизация |
|
|
|
600 |
|
Итого |
|
|
|
9000 |
Себестоимость единицы услуг гаража ![]()
Если данную модель обобщить на случай любого числа подразделений, то она обеспечит прозрачность затрат. Действительно, если есть сомнения в достоверности цифр в смете затрат, (например, кажется высокой себестоимость заложенных услуг прачечной в смете гаража), можно рассмотреть документ (смету прачечной), где ее себестоимость рассчитана.
Прежде чем функционально обобщать данную математическую модель, проведем ее анализ. Допустим, что у нас имеет N подразделений, оказывающих друг другу взаимные услуги в соответствие с заданными количествами. Обозначим через Vi и Ci заранее заданные объемы производств и подлежащие определению себестоимости услуг подразделения под условным номером i. Обратим внимание, что при взаимном удовлетворении услуг лишь часть объема используется для внутренних нужд. Для расчета этих объемов воспользуемся формулой, выведенной в работах [1,3]:
![]() (4)
(4)
Здесь ![]() доля объема услуг подразделения под условным номером i, который расходуется
на собственные нужды,
доля объема услуг подразделения под условным номером i, который расходуется
на собственные нужды, ![]() -
норма расхода услуг подразделения j на единицу объема производства услуг i.
Перепишем формулу (3) в следующем виде
-
норма расхода услуг подразделения j на единицу объема производства услуг i.
Перепишем формулу (3) в следующем виде
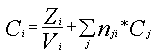 (5)
(5)
Здесь ![]() -
часть полных затрат, независящих от себестоимости услуг подразделений. Докажем
следующее тождество:
-
часть полных затрат, независящих от себестоимости услуг подразделений. Докажем
следующее тождество:
![]() (6)
(6)
Для доказательства этого воспользуемся (5). Перенесем второе слагаемое
в левую часть, умножим обе части равенства на ![]() и просуммируем по свободному индексу i:
и просуммируем по свободному индексу i:
![]() (7)
(7)
Так как суммирование у нас конечное, то его порядок роли не играет, и мы можем, поменяв индексы суммирования, преобразовать (7) к виду:
![]()
Подстановка вместо внутренней суммы выражения из (4) завершает доказательство утверждения. Назовем правую часть равенства (7) полными внешними расходами предприятия (расходы на взаимные услуги имеют смысл собственных нужд). Заметим, что для расчета полной себестоимости некоторой продукции необходимо ее себестоимость умножить на объем производства. Таким образом, доказана теорема (о соотношении между полными расходами и полной себестоимостью услуг подразделений предприятия):
Теорема
Сумма полных внешних расходов предприятия совпадает с суммой полных
себестоимостей услуг всех подразделений при условии, что в качестве объема производства
рассматриваются только часть - без собственных нужд.
Данная теорема показывает, каким образом корректно перераспределять затраты вспомогательных подразделений на основную продукцию: из сметы необходимо исключить затраты на собственные нужды.
Рассмотрим для иллюстрации пример. Пусть у предприятия имеется всего одно вспомогательное подразделение, которое может оказывать услугу само себе. То есть N=1. Опуская индексы, из формул (4), (3) получим:
![]()
или
![]() (8)
(8)
При n—>1 (подразделение работает только на себя) себестоимость его услуг стремится к бесконечности. Если не корректировать объем, то полные затраты должны бесконечно расти, что абсурдно. Однако надо учесть, что объем, идущий на собственные нужды (VH), стремится к V, а себестоимость соотносится с объемом, определяемым по формуле
![]() (9)
(9)
Произведение себестоимости на оставшийся объем равно постоянной величине Z и противоречие снимается.
Обобщим далее допущения, заложенные при формировании смет затрат. Будем считать, что при производстве одна продукция не просто использует другую продукцию, но использует ее по конкретной статье затрат. В частности, продукция может использоваться не по одной статье, что породит несколько строчек в таблице 2 с одинаковыми значениями полей "кто" и "кому". Введем в таблицу 2 еще одну колонку под названием Статья:
Таблица 8
|
Кто |
Кому |
Количество |
Цена |
Сумма |
Статья
|
|
1 |
2 |
3 |
4 |
5 |
6 |
В этом случае к уже имеющемуся анализу появляется дополнительная
возможность получения итоговых затрат в разрезе статейii. Важно то,
что если эту информацию собирать от разных пользователей в единой базе (таблице
типа 5, дополненной еще одной колонкой 6 таблицы 3), то в ней легко выделить
все внешние затраты предприятия. Для этого достаточно исключить записи, у которых
значение поля "КТО" не равно 0.
Отметим, смета однозначно связывается с подразделением, что позволяет относительно
просто собрать в одной таблице большинство статей затрат предприятия. Это обеспечивается
принципом - одно подразделение выпускает единственный вид услуг (продукцию).
Практически это похоже на котловой вид учета затрат [7]. В действительности,
подразделение может выпускать многономенклатурную продукцию. Чтобы иметь возможность
продолжать собирать все затраты в одной таблице, введем понятие калькуляция.
Во-первых, смета, это частный случай калькуляции. Во-вторых, для калькуляций
определено три варианта преобразования их затрат.
Первый вариант- ссылка. Одна калькуляция в качестве затрат использует другую калькуляцию в соответствие с заданной нормой, либо в заданном объеме. Такой вариант уже рассматривался выше при составлении баланса услуг.
Второй вариант заключается в том, что какой бы ни был объем производства одной из продукций, он полностью будет использован при производстве некоторых других продукций в долях, закон распределения которых известен. Этот вариант назовем разделением.
И последний - третий вариант состоит в том, что какие бы не были объемы производств нескольких (заранее выделенных) продукций они полностью идут на производство другой (конкретной) продукции. Этот вариант назовем объединением.
Выразим вышеописанные рассуждения аналитическими соотношениями. Используем термины теории графов [9]. Представим себе процесс производства в виде взвешенного графа (рис. 1), узлами которого являются сами продукции (их калькуляции), а входящими дугами - статьи затрат, из которых состоит калькуляция.
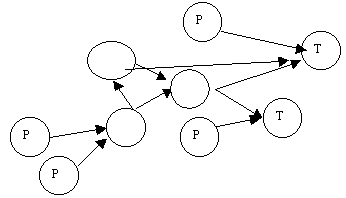
Рис. 1
Узлы (вершины), не имеющие исходящих ребер назовем товаром (Т - это последний этап переработки продукций), а узлы без входящих дуг назовем ресурсами (Р - на них нет калькуляций).
При планировании процесса производства руководство желает получить ответы на следующие главные вопросы. Во-первых, что для этого надо (какие ресурсы и в каком количестве), и во- вторых, какова будет себестоимость продукции. Для решения этих задач продолжим построение модели на графах.
Свяжем с каждым элементом графа две величины (вес дуги и вершины)
- деньги и количество. Для некоторых калькуляций понятие "количество"
может не иметь смысла. Например - затраты на амортизацию. В этом случае мы будем
отождествлять затраты в рублях и количественные затраты. Если воспользоваться
таблицей 5, то веса дуг определяются содержимым колонок 3 (количество) и 5 (деньги).
Пронумеруем узлы. С каждым узлом свяжем его условный номер i,
объем производства ![]() и
полную себестоимость
и
полную себестоимость ![]() Обозначим через
Обозначим через ![]() -
число дуг на входе, а через
-
число дуг на входе, а через ![]() -
число дуг на выходе вершины i. Будем считать, что для входящих дуг имеют место
законы сохранения денежных, а для исходящих - объемных ресурсов. Именно для
каждой вершины графа сумма затрат в рублях на входе равна полным затратам этой
вершины. Аналогично, но для исходящих дуг - для объемов. Математически это записывается
следующим образом:
-
число дуг на выходе вершины i. Будем считать, что для входящих дуг имеют место
законы сохранения денежных, а для исходящих - объемных ресурсов. Именно для
каждой вершины графа сумма затрат в рублях на входе равна полным затратам этой
вершины. Аналогично, но для исходящих дуг - для объемов. Математически это записывается
следующим образом:
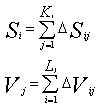 (10)
(10)
Здесь символ ![]() и
обозначает "долю" вклада одного вида продукции в себестоимость другой
и одновременно вес (в рублях) дуги, исходящей из вершины j, и входящей в вершину
i. Величина
и
обозначает "долю" вклада одного вида продукции в себестоимость другой
и одновременно вес (в рублях) дуги, исходящей из вершины j, и входящей в вершину
i. Величина ![]() представляет количество (объем) продукции J, идущей на производство продукции
i, и одновременно вес соответствующей дуги в количественном выражении.
представляет количество (объем) продукции J, идущей на производство продукции
i, и одновременно вес соответствующей дуги в количественном выражении.
Пусть заданы две таблицы, описывающие, какие продукции являются делимыми, и на какие каждая из них разделяется. Аналогично для суммируемых продукций:
Таблица 9
|
Разделяемые |
Связанные делимые |
Коэффициенты сложности |
Задаваемые затраты |
|
1 |
2 |
3 |
4 |
Таблица 10
|
Суммируемые |
Объединяемые |
Коэффициент |
Задаваемый объем |
|
1 |
2 |
3 |
4 |
Содержимое колонки 4 в каждой из таблиц показывает значения соответствующих величин, которые задаются заранее (такая ситуация допускается). Заметим, для расчетов объемов и себестоимостей узлов и дуг достаточно рассчитать эти характеристики только для дуг. Величины для узлов определяются соотношениями (10).
Возьмем произвольную дугу графа и проанализируем узлы, из которого она исходит, и в который входит. В дальнейшем, если не оговорено иначе, будем считать номером J, откуда дуга исходит и I, куда входит.
Пусть узел I является продукцией, распределяемой по нормированному закону, тогда
![]() (11)
(11)
![]()
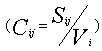 (12)
(12)
Рассмотрим теперь другие ситуации и проанализируем отдельно соотношения
для определения объемов и себестоимостей.
Дополнительную информацию Вы можете получить в компании Interface Ltd.
Обсудить на форуме
Отправить
ссылку на страницу по e-mail
| Interface Ltd. Отправить E-Mail http://www.interface.ru |
|
| Ваши
замечания и предложения отправляйте
автору По техническим вопросам обращайтесь к вебмастеру Документ опубликован:22.03.02 |