| СТАТЬЯ |
21.05.03
|
© Хрусталёв Е.М.
Алеф Консалтинг & Софт
Статья посвящена формализации механизма агрегации данных OLAP-куба с использованием теории множеств и теории графов. В ходе изложения выводятся формулы количества агрегатов при полной и частичной агрегации, а также на основании полученной сетевой модели рассматриваются вопросы оптимальности процедур предварительного и оперативного формирования агрегатов.
Содержание
Нет необходимости говорить об актуальности систем поддержки многомерного оперативного анализа данных или OLAP-систем. Об этом на данный момент существует уже и так достаточно много публикаций. В основном, доступная литература, касающаяся данной тематики, посвящена концепции, технологиям OLAP, а также вопросам практического характера. Вот чём действительно мало материала, так это о теоретических основах OLAP. Возможно, из-за этого достаточно широко распространено мнение о том, что OLAP-системы не представляют интереса с математической точки зрения.
Статья посвящена формальному представлению механизма агрегации данных OLAP- куба, а, следовательно, большинство фактов изложено математическим языком, поэтому материал статьи рассчитан в первую очередь на круг читателей, глубоко интересующихся проблемами OLAP-систем.
Прежде, чем мы перейдем непосредственно к вопросам агрегации данных, напомним основные понятия многомерной модели данных, характерной для OLAP- систем. Дело в том что, на данный момент нет общепризнанной точки зрения на многомерную модель представления данных. Конечно, принципиальных различий в существующих взглядах нет, однако с точки зрения, например, терминологии некоторые разногласия имеются. Мы в данной статье будем ориентироваться на вариант, предлагаемый компанией “Microsoft”.
Итак, основными понятиями многомерной модели данных являются:
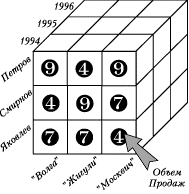
Измерения играют роль индексов, используемых для идентификации значений показателей, находящихся в ячейках гиперкуба. Комбинация членов различных измерений играют роль координат, которые определяют значение определенного показателя (рис.2). Поскольку для куба может быть определено несколько показателей, то комбинация членов всех измерения будет определять несколько ячеек со значениями каждого из показателей. Поэтому для однозначной идентификации ячейки необходимо указать комбинацию членов всех измерений и показатель.
Рис. 1 Куб c тремя измерениями
Заметим, что, в отличие от измерений, не все значения показателей должны иметь и имеют реальные значения. Например, Менеджер Петров в 1994 г. мог еще не работать в фирме, и в этом случае все значения Показателя Объем продаж за этот год будут иметь неопределенные, “пустые” значения.
Иерархии в измерениях необходимы для возможности агрегации и детализации значений показателей согласно иерархической структуре.
Существуют следующие типы иерархий:
Описанная в данном документе модель агрегации данных предназначена только для сбалансированных иерархий, однако это не является существенным ограничением, поскольку несбалансированные и неровные иерархии встречаются достаточно редко по сравнению со сбалансированными.
Степень агрегации куба вычисляется как:
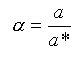(1)
где a – реальное количество агрегированных значений показателей, a* - максимально возможное количество агрегатных значений исходных данных куба.
При выводе формул для a и a* сначала будем разбирать простые случаи с двумя-тремя измерениями, а затем перейдём к обобщённому варианту. То же самое касается и уровней иерархии в измерениях: сначала рассматриваются случаи простых измерений (с одним уровнем), а затем на примере измерений с несколькими уровнями выводится обобщённая формула. Такой подход позволяет легче понять процесс получения агрегатных значений показателей, поскольку читателю легче представить себе двух и трёхмерное пространство, сем пространства большей размерности.
Для начала исследуем случай с тремя простыми измерениями. Для большей наглядности рассмотрим пример учёта объёма продаж автомобилей. Структура многомерного куба будет включать в себя следующие объекты:
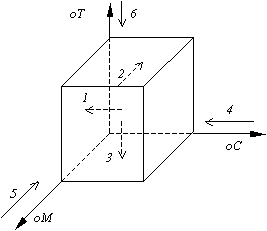
Рис. 2 Трёхмерный OALP-куб с простыми измерениями; стрелки показывают направление агрегации.
Обозначим С, М, T – множества членов соответствующих измерений “модели автомобилей”, “менеджеры”, “месяцы”. Обозначим также количество членов в каждом из измерений nс = |С|, nm = |М|, nt = |T|. Члены этих измерений будем обозначать соответственно mc, mm, mt.
Для получения агрегированных значений в разрезе менеджеров и месяцев мы должны просуммировать первоначальные значения показателей по всем моделям для каждой комбинации (mt, mm) менеджеров и месяцев. На рис.2 направление агрегирования обозначено стрелкой 1. Нетрудно понять, что количество агрегированных таким образом значений равно nmnt . Можно представить, что агрегированные таким образом значения показателей располагаются на плоскости (oM, oT)
Аналогично рассуждая, получим число агрегатов для всех комбинаций mc, mt) при суммировании показателей по всем членам измерения “менеджеры”. Оно равно ncnt.
Количество агрегатов для всех комбинаций (mc, mm) при агрегации по временному измерению равно nm nc.
Теперь необходимо получить число агрегатов в разрезе членов одного из измерений. Очевидно, что количество таких агрегатов равно числу членом соответствующего измерения nm, nc и nt.
Учитывая значение полного агрегата, определяющее в нашем случае суммарный объём продаж по всем моделям, менеджерам и всему временному периоду, получим суммарное количество всех агрегатов:
a* = nmnc + ncnt + nmnt + nc + nm + nt + 1
Для дальнейших рассуждений введём новые обозначения. Допустим, имеем m измерений с ni количество членов в i-ом измерении, где i = 1..m. Упорядочим некоторым образом существующие измерения и сопоставим каждому измерению порядковый номер i в соответствии с указанной сортировкой. Обозначим множество таких порядковых номеров I, так что m = | I |.
Обозначим некоторое множество агрегатов через Al1…li…lm , где liЕ{0,1}: выделим также такое подмножество порядковых номеров I0= {ik | ikEI & lik= 0 }, k = 1…p, p<= m. Тогда будем считать Al1…li…lm – множество агрегатов, полученных агрегированием по всем членам тех измерений, порядковый номер которых iЕI0.
Тогда A1…1, где индексы во всех позициях равны 1, является множеством исходных данных; A0…0, где индексы во всех позициях равны 0, содержит единственное значение полного агрегата.
Упорядоченную последовательность l1,…,li,…,lm , соответствующую множеству агрегатов Al1…li…lm, будем называть состоянием агрегации.
Введем понятие уровня детализации l = l1+…+li+…+lm. Очевидно, разные состояния агрегации, а, следовательно, и множества агрегатов могут соответствовать одному и тому же уровню детализации.
Обозначим количество агрегатов множества Al1…li…lm, как al1…li…lm = |Al1…li…lm|.
Для нашего трёхмерного случая с учётом того, что i(C)=1, i(M)=2, i(T)=3 – порядковые номера измерений, получим
a011= nmnt a101= ncnt a110= ncnm a001= nt a010= nm a100= nc,
тогда a* = a011+ a101+ a110 + a001+ a010 + a100 + a000.
Легко понять, что количество агрегатов, полученных агрегированием по некоторым измерениям, равно произведению числа членов всех остальных измерений, то есть
(2)
Очевидно, что количество всевозможных агрегатов равно сумме al1…li…lm при всевозможных вариантов последовательности l1,…,li,…,lm, исключая множество исходных данных . Нетрудно понять, что таких вариантов всего 2m -1.
С другой стороны при агрегации исходных данных по всевозможным k измерениям, где k E {1,…,m}, мы получаем некоторую совокупность множеств агрегации с одним и тем же уровнем детализации, равным l = m - k. Обозначим эту совокупность Al, с количеством агрегатов al. Для расчёта количества множеств агрегации Al1…li…lm в Am-k нам необходимо в индексе посчитать количество вариантов размещения k нулей по m позициям. Это случай сочетания k элементов по m, равный Ckm. Таким образом,
,
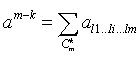где |I0| = k. Легко понять, что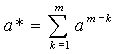
,
поэтому формула расчёта полного числа агрегатов с учётом (2) может быть представлена
следующим образом
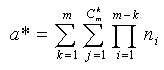(3)
где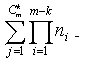
сумма всевозможных неповторяющихся произведений количества членов измерений.
Гораздо более простую с точки зрения представления и вычисления формулу можно получить, используя свойство, вытекающее из (2):
Al1…li-1 1 li+1…lm = ni Al1…li-1 0 li+1…lm
Тогда получим следующее
Исключая число исходных данных, получим
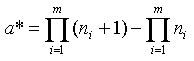(4)
Теперь рассмотрим случай, когда для i-го измерения существует li* уровней иерархии.
Обозначим nij – количество членов в j-ом уровне i-го измерения,
так что ni
j1Ј ni j2 при j1 меньше j2; общее количество членов i-го измерения
как ni, так что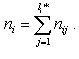
.
Упорядочивая измерения некоторым образом, получим последовательность измерений D1,...,Di,...,Dm , где i – порядковый номер измерения. Обозначим множество таких номеров I.
Определим последовательность чисел 11,…,li,…,lm таких, что 1i = 0...li*, как состояние агрегации. Тогда Al1…li…lm – множество агрегатов, полученных агрегированием исходных данных до li-го уровня каждого из m измерений, al1…li…lm = |Al1…li…lm|. Как и случае с простыми измерениями, обозначим подмножество порядковых номеров I0= { ik | ikОI & lik= 0 }, k=1…p, p<= m.
Уровень иерархии с нулевым номером 1i = 0 можно ассоциировать с абстрактным корневым уровнем, содержащим всегда единственный член (ni0 =1), который, как правило, не имеет соответствия реальному объекту предметной области. В таком случае агрегацию по всем членам i-го измерения можно интерпретировать, как агрегацию до корневого уровня i-го измерения.
Как и в случае с простыми измерениями, назовем уровнем детализации, соответствующее множеству агрегатов Al1…li…lm число l = l1+…+li+…+lm.
Рассмотрим двухмерный случай со следующей структурой:
Пусть количество членов временного измерения (T) превышает количество членов измерения функциональных единиц (U) Тогда
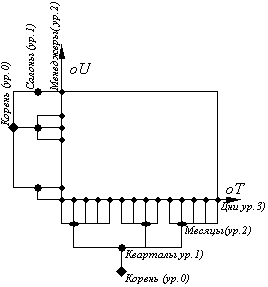
Рис 3 Двухмерный случай с иерархическими измерениями
Нетрудно понять, что количество агрегатов:
Таким образом
a* = n12 n22 + n13 n21+ n13+ n12 n21+ n11 n22+ n12+ n11 n21+ n22, + n21 + n11 + 1.
Из определения Al1…li…lm следует, что
(5а),
что является общим случаем относительно формулы (2). Учитывая, что ni0 = 1, получим более простую формулу
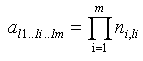(5б)
Из (5б) получим соотношение между мощностями с различными уровнями детализации
ni,li-k al1…li…lm = ni,li al1…li-k…lm (6) , где li = k…li*.
Общее количество всех агрегатов получается суммированием числа агрегатов множеств Al1…li…lm, определяемых всевозможными состояниями агрегации. Число комбинаций l1,…,li,…,lm без учёта комбинации, соответствующей исходным данным, равно произведению (l1*+1)… (li*+1)… (lm*+1) – 1. Тогда с учётом (5б) получим количество всевозможных агрегатов:
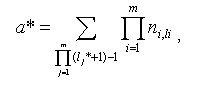
где каждое слагаемое представляет уникальное произведение числа членов измерений.
Получим более удобную с точки зрения вычисления формулу количества всевозможных агрегатов. Для этого свойством
следующим из (6). Рассмотрим сумму всевозможных al1…li…lm.
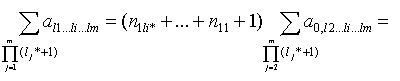
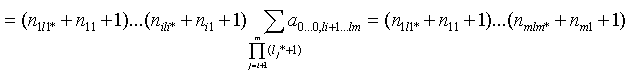
Исключая множество исходных данных, и учитывая, что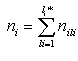
, получим
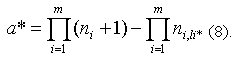
Как нетрудно заметить, формула (8) представляет обобщённый вид формулы (4).
Введём оператор агрегирования A по i-му измерению, преобразующий множество агрегатов, которым в том числе может являться множество исходных данных, в другое множество агрегатов, уровень иерархии которого в i-ом измерении на единицу меньше по сравнению с исходным множеством, так что
Из определения оператора агрегирования следует:
Под вычислительными затратами на выполнение агрегации некоторого множества
значений показателей (агрегированных или исходных) до определенного результирующего
множества агрегатов будем понимать количество элементарных операций суммирования,
которые необходимо осуществить для получения результирующего множества. Будем
обозначать затраты на выполнение агрегирования множества Al1…li…lm по i-му
измерению, как C(A(i, Al1…li…lm)) или более коротко
C(i, Al1…li…lm).
Очевидно, что C(i, Al1…l(i-1),0, l(i+1)…lm) = 0
Ещё раз обратимся к вышеописанному случаю с тремя простыми измерениями. Для формирования множества агрегатов A011 для каждой комбинации менеджеров и месяцев необходимо просуммировать исходные значения показателей по направлению стрелки 1 (рис. 2) nc-1 раз. Таким образом, с учётом того, что i(C) =1, i(M)=2, i(T) =3 – порядковые номера измерений, затраты на выполнение агрегирования A(1, A111) = A011 определяются как C(1, A111) = (nc - 1)nmnt.
Аналогично при формировании множеств агрегатов A101 и A110 на основании исходных значений показателей получим соответственно затраты
C(2, A111) = nc nt (nm - 1) и C(2, A111) = nc nm (nt –1).
Получение множества A001 согласно третьему заключению из определения оператора агрегации возможно двумя способами:
Очевидно, что затраты на эти операции различны и равны соответственно
C(1, A101) = (nc-1)nt, и C(2, A011) = (nm-1)nt.
Эту неоднозначность при оценке затрат при формировании множества агрегатов мы обсудим ниже.
Покажем, как рассчитываются затраты на агрегирование в общем случае с иерархическими измерениями. Для этого используем следующее утверждение.
Утверждение 1 Пусть существует иерархия с l* уровнями, где nl – количество членов на l-ом уровне и nl<=nl+1 l = 1…l*-1. Тогда количество элементарных операций суммирования значений показателя, соответствующих l+1-му уровню, с целью получения агрегированных значений показателя l-го уровня равно nl+1 - nl.
В нашем примере с двумя иерархическими (рис. 3) измерениями для получения агрегированных значений показателя по каждой комбинации менеджеров и месяцев (А22) необходимо провести агрегацию множества исходных A32 данных по временному измерению А22 = A(1, A32). Для этой операции необходимо для каждого менеджера просуммировать значения показателя по дням с целью получения показателя по месяцам (согласно утверждению) n13 - n12 раз. Таким образом,
C(1, A32) = (n13 – n12)n22 = n13 n22 - n12 n22 = a32 - a22.
Аналогично затраты на агрегацию значений показателя в разрезе менеджеров и кварталов по временному измерению с целью получения агрегатов только по менеджерам равны
C(1, A12) = (n11 – n10) n22 = (n11 – 1) n22 = n11 n22 - n22 = a12 = a02,
Обобщая выше описанные примеры, заключим, что при суммировании множеств агрегатов по i-му измерению с li-го на li-1 уровень необходимо для каждой комбинации из членов текущих уровней всех остальных m-1 измерений провести ni,li – ni,li-1 элементарных операций суммирования. Таким образом, получаем
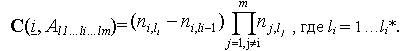
Используя (5а) и (6), преобразуем эту формулу в вид, который нам понадобится в дальнейших рассуждениях.
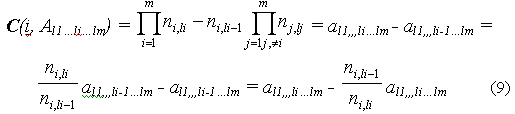
Множество агрегатов можно ассоциировать с вершинами сетевого графа. Начальной вершиной такого графа является множество исходных данных, конечной – значение полного агрегата (рис. 4)
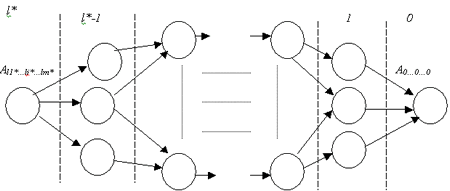
Рис.4 Представление множества агрегатов в виде сетевого графа
В любое множество агрегатов Al1…li…lm (li E {0,… li*-1}) можно непосредственно перейти из другого множества Al1…li+1…lm, произведя операцию агрегирования по i-му измерению. При этом необходимо произвести соответствующие вычислительные затраты, откладываемые на рёбрах графа.
Можем также высказать следующее утверждение.
Утверждение 2 В любую вершину графа Al1…li…lm можно попасть из другой вершины Al1’…li’…lm, если хотя бы одно из неравенств li’=> li , i = 1…m выполняется строго.
Теперь перейдём непосредственно к процедуре предварительного формирования агрегатных значений исходных данных куба известной структуры так, чтобы степень агрегации рассматриваемого куба достигла значения ?. Для этого согласно (1) необходимо сформировать a=aa* агрегатов. Ниже описаны основные моменты, характеризующие процедуру предварительного формирования агрегатов.
Принцип “от детального к общему”. Очевидно, что процедуру формирования агрегированных значений показателей необходимо начинать с формирования агрегатов, соответствующих большей степени детализации. Будем считать, что формирование агрегатов l-го уровня детализации невозможно без получения всевозможных агрегатов l+1-го уровня детализации.
Принцип минимальных затрат. Как же было сказано ранее, расчёт множества агрегатов Al1…li…lm может быть возможен нескольким способами:
Al1…li…lm = {A(i, Al1…li-1…lm) | i = 1…m & li= 0…li* - 1},
причём затраты на каждую из этих операции агрегации различны. Логично из всех возможных альтернатив агрегации выбирать ту, которая требует наименьших вычислительных затрат.
Распределение агрегатов между множествами одного уровня детализации. Рассмотрим совокупность множеств агрегации Al, соответствующих уровню детализации l ( l=1…1*). Допустим, к настоящему моменту все множества большей степени детализации, чем l, сформированы и общее их количество равно a’. Обозначим множество всех агрегатов уровня l как al. В зависимости от заданной для текущего куба степени агрегации возможны следующие варианты дальнейшего поведения.
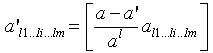
Правило, по которому определяется, какие из агрегатов в каждом множестве Al1…li…lm формируются, а какие нет, не регламентируется, так что формируемые агрегаты выбираются случайным образом.
Описанная процедура, возможно, и обеспечивает минимальные вычислительные затраты на её выполнение, но она далеко не оптимальна по отношению к множествам формируемых агрегатов. Для пояснения этого факта рассмотрим процедуру оперативного формирования агрегатов.
Будем понимать под процедурой оперативного формирования агрегатов процедуру получения результирующего набора агрегатов при выполнении пользовательского запроса. При расчёте результирующего набора агрегатов будут использоваться подходящие предварительно сформированные агрегированные значения показателей. Если результирующий набор агрегатов предварительно сформирован, то затраты на оперативное формирование агрегатов равны 0.
Ясно, что для получения множества агрегатов определённого уровня, необходимо вначале получить множества агрегатов большего уровня детализации. Однако в отличие от процедуры предварительного формирования агрегатов при получении результирующего набора нет необходимости формировать всевозможные агрегаты определённого уровня детализации. Достаточно формировать по одному множеству определённого уровня на основе множества более детального уровня.
Пусть в результате процедуры предварительно формирования агрегатов получили всевозможные множества минимального уровня детализации l. Пусть в результате необходимо сформировать множество агрегатов Al’1,…,l’m уровня детализации l’, l’< l. Необходимо на основании одного из множеств Al1,…,lm l–го уровня получить результирующее множество. При этом:
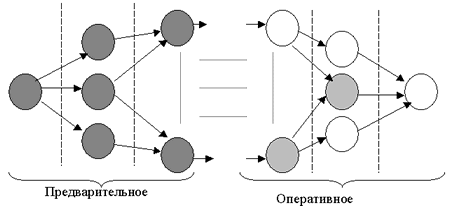
Рис.5. Предварительное и оперативное формирование агрегатов в сетевой модели
Есть основания полагать, что такая процедура оперативного формирования обеспечит минимальное время выполнения пользовательских запросов. С другой стороны многое зависит и от множества предварительно сформированных агрегатов. Ясно, что они должны быть сформированы так, чтобы вычислительные затраты на оперативное формирование всевозможных множеств были минимальны. В этом и заключается упомянутая выше оптимальность процедуры предварительного формирования агрегатов.
Итак, мы формально описали механизм агрегации данных OLAP-куба. В результате чего:
Алгоритмы предварительного оперативного формирования агрегатов должны обеспечивать минимальное время выполнения всевозможных пользовательских запросов при фиксированном объёме дискового пространства, занимаемого агрегатами. Формализация механизма агрегации позволила привести эту задачу к задаче сетевой оптимизации. Безусловно, полученная модель, как и любая другая, имеет определённые ограничения и допущения, однако, по мнению автора, она существенно позволяет решать проблему роста объёма дискового пространства для хранения агрегатов в случае больших производственных OLAP- кубов.
Дополнительная информация
За дополнительной информацией обращайтесь в компанию Interface Ltd.
| INTERFACE Ltd. |
| ||||
