В данной публикации рассмотрен простой и эффективный алгоритм нормализации данных с помошью простых чисел. Нормализация данных широко используется при шифровании, архивировании данных, а также может иметь некоторые другие практические применения, поэтому я надеюсь, что изложенный в статье материал будет полезен читателям. Также, в качестве примера, приведён пример кода на языке С++ реализующий описанный в статье метод нормализации данных.
Краткое описание алгоритма нормализации данных
Ряд натуральных чисел N = {1, 2, 3, …. n}, n = 1, Ґ можно разложить в виде суммы произвольного количества рядов, следующего вида:
N = {2n+1} + {2n+2} , n = 0, Ґ
N = {3n+1} + {3n+2}+ {3n+3} , n = 0, Ґ
N = {4n+1} + {4n+2}+ {4n+3}+ {4n+4} , n = 0, Ґ
N = {5n+1} + {5n+2}+ {5n+3}+ {5n+4}+ {5n+5} , n = 0, Ґ
N = {6n+1} + {6n+2}+ {6n+3}+ {6n+4}+ {6n+5} + {6n+6} , n = 0, Ґ
Очевидно, что часть рядов составляющих сумму натурального ряда, будут содержать не более одного простого числа, которое является первым элементом последовательности и их можно исключить из рассмотрения при поиске простых чисел. Так каждая из следующих шести последовательностей будет содержать столько же простых чисел, сколько и натуральный ряд.
N2 = {2n+1} , n = 0, Ґ
N3 = {3n+1} + {3n+2} , n = 0, Ґ
N4 = {4n+1} + {4n+3} , n = 0, Ґ
N5 = {5n+1} + {5n+2}+ {5n+3}+ {5n+4} , n = 0, Ґ
N6 = {6n+1} + {6n+5} , n = 0, Ґ
Пусть P = {1,2,3,5,7,11,13,17,19,23,29, … Pn }, n = 1, Ґ ряд простых чисел. Рассмотрим представление натурального ряда в виде суммы следующего количества рядов P2 * P3 * …. * Pn , n = 2, Ґ за исключением рядов, содержащих не более одного простого числа.
Для примера на рисунке ниже наглядно показано разложение натурального ряда в виде 30-ти рядов (P2 * P3* P4 = 2*3*5 = 30), только 8-мь из которых содержат простые числа. Исключаемые из рассмотрения последовательности выделены цветом.
Рис. 1
Как видно из рисунка, после разложения натурального ряда мы получили некоторую последовательность, состоящую из 8-ми рядов и содержащую в себе все простые числа, за исключением 2, 3 и 5.
N = {30n+1} + {30n+7}+ {30n+11} + {30n+13}+ {30n+17} + {30n+19}+ {30n+23} + {30n+29} , n = 0, Ґ
Также отметим, что в полученной нами последовательности нет ни одного элемента кратного 2, 3 или 5. Очевидно, что данную последовательность можно также получить, проверяя каждое из натуральных чисел на кратность 2, 3 или 5.
Далее рассмотрим вопрос о соотношении чисел в данной последовательности к общему числу натуральных чисел. Нетрудно посчитать, что в данном случае оно равно отношению выбранного и общего количества рядов при разложении натурального ряда N, что составляет 8/30 или 26,67% от общего количества натуральных чисел.
В общем случае, данное отношение можно вычислить по следующей формуле:

В таблице ниже приведены расчеты % для различных последовательностей.
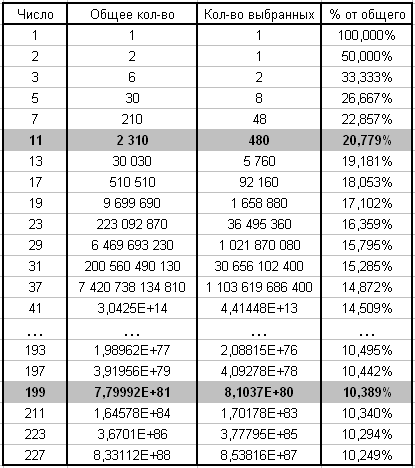
Из таблицы видно, что последовательность, не содержащая чисел кратных 2,3,5,7,11 , составляет 20,78 % натуральных чисел, а последовательность не содержащая чисел кратных 2,3,5,7,11, …, 197, 199 только 10,39 % натуральных чисел. Если числа принадлежащие только первой последовательности обозначить 0, а числа, принадлежащие и первой и второй последовательности, 1 то мы получим бесконечную периодическую последовательность из 0 и 1, элементы которой будут повторяться через 8.8E+81 . Следует отметить, что соотношение 0 и 1 в полученной последовательности будет примерно равным.
Далее приведен пример кода на С++, использующий данную последовательность из 0 и 1, для нормализации данных:
// S2310.cpp : simple data crypting algoritm
// [art & design by Dmitry Grigoriev] e-mail:bind@ngs.ru
#include <stdlib.h>
#include <fstream.h>
typedef unsigned char uint8;
typedef unsigned __int64 uint64;
class S2310
{
static const int Z[41];
static const int S[480];
static bool test(uint64 Val);
public:
static void proc(uint64 n, uint8* buf, int len); // 60 bytes max
};
const int S2310::Z[41] = { 13 , 17 , 19 , 23 , 29 , 31 , 37 , 41 ,
43 , 47 , 53 , 59 , 61 , 67 , 71 , 73 ,
79 , 83 , 89 , 97 , 101 , 103 , 107 , 109 ,
113 , 127 , 131 , 137 , 139 , 149 , 151 , 157 ,
163 , 167 , 173 , 179 , 181 , 191 , 193 , 197 , 199 };
const int S2310::S[480] = { 1 , 13 , 17 , 19 , 23 , 29 , 31 , 37 ,
41 , 43 , 47 , 53 , 59 , 61 , 67 , 71 ,
73 , 79 , 83 , 89 , 97 , 101 , 103 , 107 ,
109 , 113 , 127 , 131 , 137 , 139 , 149 , 151 ,
157 , 163 , 167 , 169 , 173 , 179 , 181 , 191 ,
193 , 197 , 199 , 211 , 221 , 223 , 227 , 229 ,
233 , 239 , 241 , 247 , 251 , 257 , 263 , 269 ,
271 , 277 , 281 , 283 , 289 , 293 , 299 , 307 ,
311 , 313 , 317 , 323 , 331 , 337 , 347 , 349 ,
353 , 359 , 361 , 367 , 373 , 377 , 379 , 383 ,
389 , 391 , 397 , 401 , 403 , 409 , 419 , 421 ,
431 , 433 , 437 , 439 , 443 , 449 , 457 , 461 ,
463 , 467 , 479 , 481 , 487 , 491 , 493 , 499 ,
503 , 509 , 521 , 523 , 527 , 529 , 533 , 541 ,
547 , 551 , 557 , 559 , 563 , 569 , 571 , 577 ,
587 , 589 , 593 , 599 , 601 , 607 , 611 , 613 ,
617 , 619 , 629 , 631 , 641 , 643 , 647 , 653 ,
659 , 661 , 667 , 673 , 677 , 683 , 689 , 691 ,
697 , 701 , 703 , 709 , 713 , 719 , 727 , 731 ,
733 , 739 , 743 , 751 , 757 , 761 , 767 , 769 ,
773 , 779 , 787 , 793 , 797 , 799 , 809 , 811 ,
817 , 821 , 823 , 827 , 829 , 839 , 841 , 851 ,
853 , 857 , 859 , 863 , 871 , 877 , 881 , 883 ,
887 , 893 , 899 , 901 , 907 , 911 , 919 , 923 ,
929 , 937 , 941 , 943 , 947 , 949 , 953 , 961 ,
967 , 971 , 977 , 983 , 989 , 991 , 997 , 1003 ,
1007 , 1009 , 1013 , 1019 , 1021 , 1027 , 1031 , 1033 ,
1037 , 1039 , 1049 , 1051 , 1061 , 1063 , 1069 , 1073 ,
1079 , 1081 , 1087 , 1091 , 1093 , 1097 , 1103 , 1109 ,
1117 , 1121 , 1123 , 1129 , 1139 , 1147 , 1151 , 1153 ,
1157 , 1159 , 1163 , 1171 , 1181 , 1187 , 1189 , 1193 ,
1201 , 1207 , 1213 , 1217 , 1219 , 1223 , 1229 , 1231 ,
1237 , 1241 , 1247 , 1249 , 1259 , 1261 , 1271 , 1273 ,
1277 , 1279 , 1283 , 1289 , 1291 , 1297 , 1301 , 1303 ,
1307 , 1313 , 1319 , 1321 , 1327 , 1333 , 1339 , 1343 ,
1349 , 1357 , 1361 , 1363 , 1367 , 1369 , 1373 , 1381 ,
1387 , 1391 , 1399 , 1403 , 1409 , 1411 , 1417 , 1423 ,
1427 , 1429 , 1433 , 1439 , 1447 , 1451 , 1453 , 1457 ,
1459 , 1469 , 1471 , 1481 , 1483 , 1487 , 1489 , 1493 ,
1499 , 1501 , 1511 , 1513 , 1517 , 1523 , 1531 , 1537 ,
1541 , 1543 , 1549 , 1553 , 1559 , 1567 , 1571 , 1577 ,
1579 , 1583 , 1591 , 1597 , 1601 , 1607 , 1609 , 1613 ,
1619 , 1621 , 1627 , 1633 , 1637 , 1643 , 1649 , 1651 ,
1657 , 1663 , 1667 , 1669 , 1679 , 1681 , 1691 , 1693 ,
1697 , 1699 , 1703 , 1709 , 1711 , 1717 , 1721 , 1723 ,
1733 , 1739 , 1741 , 1747 , 1751 , 1753 , 1759 , 1763 ,
1769 , 1777 , 1781 , 1783 , 1787 , 1789 , 1801 , 1807 ,
1811 , 1817 , 1819 , 1823 , 1829 , 1831 , 1843 , 1847 ,
1849 , 1853 , 1861 , 1867 , 1871 , 1873 , 1877 , 1879 ,
1889 , 1891 , 1901 , 1907 , 1909 , 1913 , 1919 , 1921 ,
1927 , 1931 , 1933 , 1937 , 1943 , 1949 , 1951 , 1957 ,
1961 , 1963 , 1973 , 1979 , 1987 , 1993 , 1997 , 1999 ,
2003 , 2011 , 2017 , 2021 , 2027 , 2029 , 2033 , 2039 ,
2041 , 2047 , 2053 , 2059 , 2063 , 2069 , 2071 , 2077 ,
2081 , 2083 , 2087 , 2089 , 2099 , 2111 , 2113 , 2117 ,
2119 , 2129 , 2131 , 2137 , 2141 , 2143 , 2147 , 2153 ,
2159 , 2161 , 2171 , 2173 , 2179 , 2183 , 2197 , 2201 ,
2203 , 2207 , 2209 , 2213 , 2221 , 2227 , 2231 , 2237 ,
2239 , 2243 , 2249 , 2251 , 2257 , 2263 , 2267 , 2269 ,
2273 , 2279 , 2281 , 2287 , 2291 , 2293 , 2297 , 2309 };
bool S2310::test(uint64 Val)
{
for(int i=0;i<41;i++)
{
if(Val % Z[i] == 0) return false;
}
return true;
}
void S2310::proc(uint64 n, uint8* buf, int len) // 60 bytes max
{
int num = 0;
for(int i=0;i<480;i+=8)
{
uint8 byte = 0x00;
if(test(S[i+0] + 2310 * n)) byte /= 0x01; //1;
if(test(S[i+1] + 2310 * n)) byte /= 0x02; //2;
if(test(S[i+2] + 2310 * n)) byte /= 0x04; //4;
if(test(S[i+3] + 2310 * n)) byte /= 0x08; //8;
if(test(S[i+4] + 2310 * n)) byte /= 0x10; //16;
if(test(S[i+5] + 2310 * n)) byte /= 0x20; //32;
if(test(S[i+6] + 2310 * n)) byte /= 0x40; //64;
if(test(S[i+7] + 2310 * n)) byte /= 0x80; //128;
if(num < len) buf[num++] ^= byte;
}
}
int main(int argc, char* argv[])
{
if(argc == 4)
{
uint64 count = _atoi64(argv[1]);
ifstream in(argv[2],ios::binary);
ofstream out(argv[3],ios::binary);
uint8 buf[60];
int bytes = 0;
while(!in.eof())
{
in.read(buf, 60);
bytes = in.gcount();
S2310::proc(count++, buf, bytes);
out.write(buf, bytes);
}
in.close(); out.close();
}
else
{
cout << "try:" << argv[0] << " uint64 file_src file_dst\n";
}
return 0;
}
Откомпилируйте приведённый выше код любым компилятором языка C/C++ (рекомендуется использовать MS Visual C++ ) или загрузите скомпилированную версию отсюда.
Выполните команду s2310.exe 23365444532 ваш_файл нормализованный_файл для нормализации файла. В результате получится некоторый нормализованный (зашифрованый) файл, соотношениие 0 и 1 в котором будет почти одинаковое. Число 23365444532 выбрано случайным образом, это 64-bit беззнаковое целое является ключом для востановления исходного файла. Не зная данного числа, востановить исходный файл невозможно.
Чтобы востановить исходный файл выполните команду s2310.exe 23365444532 нормализованный_файл ваш_файл
В качестве ключа для нормализации/востановления данных Вы можете использовать произвольное 64-bit беззнаковое целое число. На тестах данный метод нормализации данных показал хорошие результаты, т.е. в получаемом файле соотношение 0 и 1 всегда почти точно 50% на 50%, в не зависимости от соотношение 0 и 1 в исходном файле.

