Введение
Общество накапливает данные по экспоненциальной шкале. IBM утверждает, что 90% имеющихся сегодня данных создано только за последние два года. К счастью, существует множество методов прогностического моделирования, включая нейронные сети (NN), кластеризацию, метод опорных векторов (SVM) и ассоциативные правила, которые помогают извлекать из этих данных смысл и значение. Это делается путем обучения моделей, скрытых в больших объемах исторических данных. Результатом обучения становится прогностическая модель. После проверки модели она считается способной обобщать приобретенные знания и применять их к новым ситуациям. Методы прогностического моделирования, которые позволяют по прошлому предсказывать будущее, применяются при решении множества задач, таких как рекомендующие системы, обнаружение мошенничества и злоупотреблений или профилактика заболеваний и несчастных случаев. Наличие "больших данных" и недорогие вычислительные ресурсы расширяют применимость методов прогнозирования на основе данных в разных отраслях. При этом квалифицированные математики помогают все большему числу компаний оценить истинный потенциал, скрытый в их данных.
Прогностический анализ используется компаниями и частными лицами по всему миру для извлечения пользы из исторических данных, получаемых от людей и датчиков. К данным, получаемым от людей, относятся структурированные операции клиентов (например, онлайн-покупки) или неструктурированные данные, извлекаемые из социальных сетей. Данные датчиков поступают от массы устройств, используемых для наблюдения за дорогами, мостами, зданиями, сооружениями, электросетями, атмосферой и климатом. В этой статье мы сосредоточимся на методах прогностического моделирования. Это математические алгоритмы, которые используются для "обучения" моделей, скрытых во всех этих данных.
Когда прогностическая модель построена и проверена, считается, что она способна обобщать знания, извлеченные из исторических данных, для предсказания будущего. Например, ее можно использовать для прогнозирования риска оттока клиентов в случае данных, получаемых от людей, или риска отказа машин в случае данных от датчиков. Такие модели вычисляют рейтинг или риск путем реализации функции регрессии. Прогностические модели используются и для реализации функции классификации, когда результатом является класс или категория.
Однако независимо от типа модели, одно можно сказать наверняка: куда бы мы ни пошли и что бы ни делали, прогностические модели уже формируют наш опыт. Они рекомендуют товары и услуги, основываясь на наших привычках. Они помогают врачам принимать спасительные профилактические меры с учетом нашей восприимчивости к конкретным заболеваниям.
Рождение прогностической модели
Прогностические модели рождаются всякий раз, когда данные используются для обучения метода прогностического моделирования. Говоря формальным языком, данные + метод прогностического моделирования = модель.
Таким образом, прогностическая модель ― результат объединения данных и математики, причем обучение можно представить как создание функции преобразования набора полей входных данных в результат, или целевую переменную.
Для создания прогностической модели сначала нужно собрать набор данных, который будет использоваться для обучения. Для этого набор входных полей, представляющий, например, клиента, собирается в запись. Эта запись может содержать такие признаки, как возраст, пол, почтовый индекс, количество покупок в течение последних шести месяцев и количество возвращенных товаров, в сочетании с целевой переменной, которую можно использовать для информирования о том, менял ли этот клиент поставщика в прошлом. Запись о клиенте можно математически описать как вектор в многомерном пространстве параметров, так как для определения объекта типа клиента используются несколько параметров. Когда все записи о клиенте собраны вместе, они превращаются в набор данных, который может содержать миллионы записей. Рисунок 1 иллюстрирует двухмерное представление (с использованием параметров "возраст" и "количество приобретенных товаров") нескольких входных векторов, или клиентов.
Рисунок 1. Двумерное представление входных векторов, в котором каждый вектор, или клиент, представлен желтой звездочкой.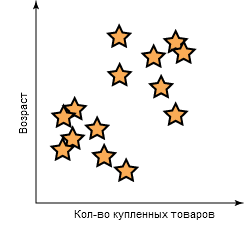
При наличии достаточного количества данных хорошего качества методы прогностического моделирования позволяют создавать точные прогностические модели. Некачественные данные приводят к плохой модели, каким бы хорошим ни был метод прогнозирования. Как говорится, из мусора получится только мусор.
Общие методы прогностического моделирования
Сегодня существует множество методов построения прогностических моделей. Разные системы и поставщики поддерживают разные методы, но полдюжины или около того методов довольно хорошо поддерживается большинством коммерческих и открытых систем построения моделей. Некоторые из них специально предназначены для решения задач определенного класса, но есть и общие методы, которые могут применяться для различных приложений. К этой категории относится, например, метод опорных векторов (SVM).
SVM отображает векторы входных данных на более многомерное пространство, где строится "оптимальная гиперплоскость", разделяющая данные. С каждой стороны от этой гиперплоскости строятся две параллельных гиперплоскости. На рисунке 2 приведен пример, в котором оптимальная гиперплоскость разделяет две категории данных (треугольники и квадраты). Оптимально разделяющая гиперплоскость определяет максимальное расстояние между двумя параллельными гиперплоскостями. Чем больше расстояние между двумя гиперплоскостями, тем точнее модель. Точки данных, лежащие на одной из двух параллельных гиперплоскостей, которые определяют наибольшее расстояние, называются опорными векторами.
Рисунок 2. Двухмерное представление оптимальной гиперплоскости, разделяющей данные и опорные вектора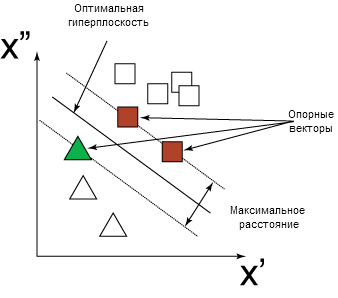
SVM, а также NN и модели логистической регрессии представляют собой мощные универсальные методы, которые хотя и различаются математически, дают в какой-то мере сопоставимые результаты. Деревья решений - еще один универсальный метод прогностического моделирования, который выделяется своей способностью объяснять смысл полученных результатов. Простые в применении и понятные, деревья решений ― наиболее популярный метод прогностического моделирования.
С другой стороны, в тех случаях, когда целевая переменная, или отклик, не имеет значения или отсутствует, очень популярна технология кластеризации. Как предполагает название, методы кластеризации способны группировать входные данные на основе сходства. На рисунке 3 показан пример, в котором входные данные разделены на две группы. Данные первой группы обозначены зелеными треугольниками, а данные второй группы ― красными квадратами.
Рисунок 3. Двухмерное представление результата кластеризации набора входных данных на группы зеленых треугольников и красных квадратов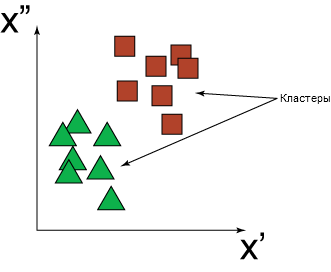
Когда целевая переменная или степень сходства не имеет значения, но важны связи между входными элементами, для их поиска может использоваться так называемый метод ассоциативных правил. Например, с помощью ассоциативных правил можно определить, что те, кто покупает подгузники и молоко, также покупают пиво.
Хотя все прогностические методы имеют свои сильные и слабые стороны, точность модели в значительной мере зависит от исходных данных и функций, используемых для обучения прогностической модели. Как упоминалось выше, построение модели в значительной мере состоит из анализа данных и манипулирования ими. Обычно из сотен полей доступных исходных данных выбирается некоторое подмножество, и до передачи в метод прогностического моделирования эти поля предварительно обрабатываются. Таким образом, секрет качественной прогностической модели часто кроется в хорошей подготовительной работе, которая даже важнее, чем метод, используемый для обучения модели. Это не означает, что от прогностического метода ничего не зависит. Если используется неподходящий метод или выбран неподходящий набор входных параметров, хорошие данные не помогут.
Например, нейронные сети могут принимать самые разные формы и форматы. Чтобы создать хорошую прогностическую модель, важно выбрать подходящую структуру сети. Как показано на рисунке 4, NN с прямой связью состоят из входного уровня, где количество узлов соответствует числу полей входных данных и рассматриваемых параметров, и выходного уровня, который в случае функции регрессии состоит из одного узла, представляющего прогнозируемое поле. Между входным и выходным уровнями нейронная сеть может иметь любое число скрытых уровней и узлов. Проблема здесь заключается в том, что если у NN будет слишком мало скрытых узлов, она не сможет обучиться функции преобразования значений входных полей в целевое значение. А слишком большое количество узлов приводит к чрезмерной подгонке, то есть модель будет в точности обучаться входным данным, но не сможет предсказывать будущие события.
Рисунок 4. Скрытые уровни и выходной уровень нейронной сети с прямой связью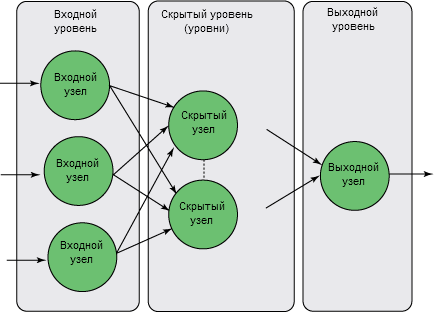
Методы кластеризации требуют, чтобы до обучения было указано некоторое количество групп, или кластеров. Если количество кластеров слишком мало, модель может упустить важные различия во входных данных, так как вынуждена объединять разные данные. С другой стороны, если количество кластеров слишком велико, она может упустить важные сходства. В примере, показанном на рисунке 3, если задать количество кластеров равным трем, а не двум, будет создан дополнительный кластер, который, вероятно, затуманит истинную природу данных (желтые треугольники или фиолетовый квадраты?).
Для прогностических моделей могут одновременно использоваться разные методы моделирования. Дело в том, что многие модели можно объединить в так называемый ансамбль моделей (рисунок 5). Результат применения такого ансамбля будет получаться с использованием преимуществ разных моделей и методов.
Рисунок 5. Схематическое представление ансамбля моделей, в котором рассчитываются оценки для всех моделей, а окончательный прогноз определяется с помощью механизма голосования или усреднения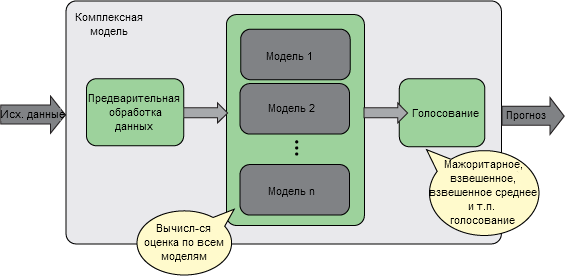
Управляемое и неуправляемое обучение
В SVM, деревьях решений, NN и регрессионных моделях для создания функции отображения между набором вводных полей данных и целевой переменной используют управляемое обучение. Известный результат используется в качестве "учителя", который контролирует обучение своих учеников. Всякий раз, когда ученик делает ошибку, учитель подсказывает правильный ответ, чтобы ученик в конечном итоге научился делать это правильно. Например, когда представлен конкретный набор входных данных, результат будет соответствовать цели.
Рассмотрим процесс обучения NN (см. рисунок 4) для прогнозирования оттока покупателей в результате истощения спроса. Для начала подберем набор полей входных данных, соответствующих конкретному покупателю, который уже ушел. Он может состоять из полей возраста, пола, а также параметров, связанных с удовлетворенностью, таких как количество жалоб. Затем этот покупатель, который теперь представлен набором полей данных и результатом (уход), используется для обучения NN. Он может представляться несколько раз, пока NN не усвоит соотношение между входными данными и целью. Однако этот покупатель не изолирован. Он всего лишь один из многих. Тот же процесс необходимо повторить для всех покупателей, как ушедших, так и оставшихся. Чтобы научиться различать два возможных результата, NN должна создать абстрактное представление о тех покупателях, которые ушли, и тех, которые остались.
Известный алгоритм обучения, используемый для NN с прямой связью, называется обратным распространением ошибки. Он позволяет ошибке, или разнице между целью и результатом, распространяться назад по сети для регулировки весовых коэффициентов синапсов, связывающих узлы сети. Таким образом, в конечном итоге сеть мало-помалу усваивает задачу. Однако такой процесс невозможен без цели.
Для неуправляемого обучения цель или учитель не требуется. В эту категорию попадают методы кластеризации. Как показано на рисунке 3, точки данных просто группируются на основе сходства. В случае оттока покупателей метод кластеризации потенциально может собрать ушедших и оставшихся в разные кластеры, несмотря на то, что во время обучения модели результат был недоступен.
Анализ методом "черного ящика"
"Черный ящик" ― это термин, используемый для определения некоторых методов прогностического моделирования, внутренняя логика которых неизвестна. Однако к этой категории относятся чрезвычайно мощные методы, такие как NN и SVM. Рассмотрим нашу высокоточную модель NN, обученную различать ушедших и оставшихся покупателей. Предсказывая высокий риск оттока для конкретного покупателя, она не позволяет понять, почему это так. Это поднимает важный вопрос: должна ли прогностическая модель объяснять логику своей работы? Все зависит от обстоятельств. В тех случаях, когда риск, указываемый прогностической моделью, используется для инициирования неблагоприятных действий, объяснение часто желательно и в некоторых случаях даже необходимо. Например, когда оценка риска используется для отклонения заявления о выдаче кредита или транзакции по кредитной карте.
Когда требуется объяснение, нужно рассматривать использование методов прогностического моделирования, которые четко обозначают причины своих решений. Для этого очень хорошо подходят оценочные таблицы. Основанные на модели регрессии, оценочные таблицы широко используются для оценки риска финансовыми учреждениями. В оценочных таблицах всем полям данных входной записи ставятся в соответствие коды конкретных причин. Во время обработки поля данных взвешиваются по отношению к базовой оценке риска. Когда определены поля, оказывающие наибольшее влияние на конечный результат, вместе с выходными данными возвращаются соответствующие коды причин.
Деревья решений так же легко объяснимы и наглядны, как и оценочные таблицы. В случае деревьев решений процесс представлен набором понятных человеку условий, то есть набором правил. Конечный узел в дереве решений достигается при соблюдении определенного набора условий. На рисунке 6 приведено графическое представление дерева решений, используемого для деления растений семейства ирисовых на три разных класса в зависимости от длины лепестков. Целевые классы: Iris-Setosa, Iris-Virginica и Iris-Versicolor. Обратите внимание, что дерево может быть представлено набором правил. Например, правило для выявления растений Iris-Setosa гласит: "Если длина лепестков меньше 2,6, то это Iris-Setosa с вероятностью 1".
Рисунок 6. Простое дерево решений, используемое для классификации растений семейства ирисовых. Возможные классы: Iris-Setosa, Iris-Virginica и Iris-Versicolor.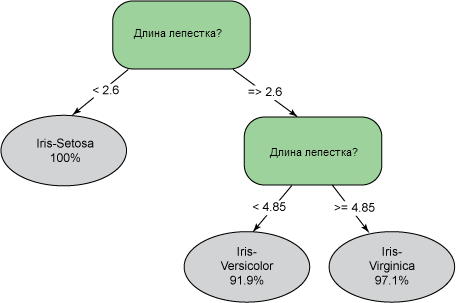
Хотя мотивы решений, найденных методами моделирования на основе "черного ящика", объяснить трудно, к самим моделям это не относится. К счастью, представление данных для предварительной обработки и самих прогностических моделей легко осуществляется с помощью языка разметки прогностических моделей PMML (Predictive Model Markup Language). Это стандарт де-факто, используемый всеми ведущими аналитическими компаниями для создания и применения прогностических решений. Он позволяет представлять в едином, стандартном формате все прогностические методы, упомянутые в этой статье. Представленную в виде PMML-файла прогностическую модель можно перенести со стола аналитика прямо в рабочую среду. Таким образом, можно оперативно внедрять новые модели или обновлять существующие. Как открытый стандарт, понятный всем, PMML используется в качестве моста не только между разработкой моделей и внедряемыми системами, но и между всеми людьми, участвующими в процессе анализа внутри компании. Он обеспечивает прозрачность и распространение знаний и передового опыта.
Нас окружает постоянно расширяющееся море данных, и анализ позволяет нам безопасно ориентироваться в нем. Исторические данные, собранные от людей и датчиков, преобразуют наш мир, позволяя создавать модели, пригодные для предсказания будущего. Эти так называемые прогностические модели, по сути, являются продуктом рациональных математических методов, применяемых к данным.
NN, SVM, деревья решений, линейная и логистическая регрессия, кластеризация, правила ассоциаций и оценочные таблицы ― вот наиболее популярные методы прогностического моделирования, используемые учеными для изучения моделей, скрытых в данных. Эти методы способны к обучению и обобщению, но требуют хороших данных и, как правило, потребляют много вычислительных ресурсов. По этой причине прогностические решения только теперь переживают бум во всех отраслях ввиду появления: 1) больших объемов данных, получаемых от людей и от датчиков; 2) экономичных платформ обработки, таких как платформы на базе облака и Hadoop; и 3) PMML, изящного и зрелого открытого стандарта представления любых прогностических решений. Вместе эти три фактора привели к появлению мощных моделей, которые можно сразу применять для принятия решений в компании любого размера.
Аналитики проделали большую работу, создавая прогностические решения для работы с данными, которые мы, как общество, собираем во все большем количестве. В сочетании с эффективными методами анализа эти данные дают нам возможность создать более рациональный мир, в котором преступность, болезни и несчастные случаи можно не только предсказывать, но и предотвращать.
