После выполнения ряда операций с упорядоченным деревом, вставки и удаления
узлов, оно может стать несбалансированным. Если подобное происходит, алгорит-
мы обработки дерева становятся менее эффективными. При сильной степени раз-
балансировки дерево фактически представляет собой всего лишь сложную форму
связанного списка, а у программы, использующей дерево, может резко снизиться
производительность.
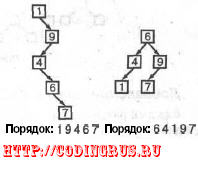
Высокие, тонкие деревья, такие как дере-
во, изображенное слева, могут иметь глубину
до O(N). Добавление или размещение элемен-
та в таком разбалансированном дереве может
занимать O(N) шагов. Даже если новые эле-
менты размещаются беспорядочно, в среднем
они дадут дерево с глубиной N/2, обработка
которого потребует так же порядка O(N) опе-
раций.
Предположим, что вы строите упорядочен-
ное двоичное дерево, содержащее 1000 узлов.
Рис. 7.1. Деревья, построенные в различном порядке
Если дерево сбалансировано, высота дерева будет порядка Iog2(1000), или при-
близительно 10. Добавление нового элемента к дереву будет занимать 10 шагов.
Если дерево высокое и тонкое, его высота равна 1000. В этом случае для вставки
нового элемента потребуется 1000 шагов.
Теперь предположим, что вы хотите добавить еще 1000 узлов. Если дерево ос-
тается сбалансированным, все 1000 узлов будут размещены на нескольких уров-
нях дерева. При этом для добавления новых элементов потребуется приблизитель-
но 10 * 1000 = 10 000 шагов. Если дерево было не сбалансировано и остается таким
в процессе роста, то при вставке каждого нового элемента оно будет становиться
все выше. Добавление элементов займет приблизительно 1000 + 1001 + ... + 2000 =
= 1,5 млн шагов.
Хотя неизвестно, в каком порядке элементы будут добавляться и удаляться из
дерева, в любом случае можно использовать методы, которые поддержат его сба-
лансированным.

Балансировка деревьев
Источник: codingrus
Kest