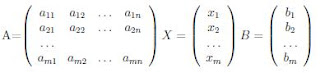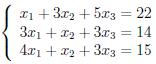Расчёты бывают разной сложности: проверить, сколько будет 6*6, посчитать сумму стоимости товаров в чеке, решить систему линейных уравнений для домашней работы, или, скажем, рассчитать деградацию волнового фронта при прохождении многослойной турбулентной атмосферы. Если первые два примера можно посчитать на любом калькуляторе, то линейные уравнения решают инженерные калькуляторы. Последний пример могут решить только системы численных расчётов, которые используют для научных исследований - например GNU/Octave. Вот о ней-то в этом посте и рассказывается.
Пояснения и предупреждения
Octave и MATLAB - это не просто "программа-калькулятор, которая может посчитать матрицу". Это интерактивные среды разработки и интерпретаторы языка в одном флаконе. На Октаве\Матлабе не просто считают матрицы - на них пишут программы. Нужно это для того, чтобы быстро набросать или протестировать новый алгоритм обработки изображений, сигналов, можно задизайнить цифровой контроллер или написать целый оптический симулятор.
Так что если вы не студент технического ВУЗа или университета, Octave вам скорее всего не нужна. Но для изучения линейной алгебры или теории вероятности Octave будет просто бесценна - собственно, на ней можно попробовать вычислить то, чему вас учили (и кучу всего, чему не научат) на курсе матричной\линейной алгебры.
Увы, но вопреки желаниям радетелей опенсорса, Octave это не замена MATLAB ни единого раза - это как старый ушастый Запорожец не замена для Lamborgini Diablo. Хотя и то, и то - ездит. Если даже после этих предупреждений вы твёрдо уверены, что оно вам надо - переходим к установке.
Установка GNU/Octave в Debian GNU/Linux
Для нормальной работы нам нужна Octave 3.0 и выше, так что если в ваших репозиториях всё ещё валяется хлам в виде Octave 2.1 - не надо его ставить. Перед установкой пакетов лучше поискать:
apt-caсhe search octave
и установить самую свежую версию. Установка довольно проста:
aptitude install octave3.0 qtoctave
Первый пакет - собственно, система численных математических рассчётов GNU/Octave, а второй - это графическая оболочка QtOctave, о которой был отдельный пост.
Для Windows сборка Octave тоже есть, и тоже бесплатная. Кроме того, под Windows есть и графический интерфейс для Octave - GUIOctave, доступный по этой ссылке. Другие графические оболочки для октавы обсуждаются тут.
Всё вместе занимает около 50Мб на диске, но красота требует жертв:
 |
| From Debianist Notes: Так выглядит QtOctave |
Установка Octave в Windows хорошо проиллюстрирована здесь в красивых цветастых картинках. Правда, после всего этого вас встретит чёрная страшная консоль Octave:
 |
| From Debianist Notes: |
Тем не менее, такой брутальный интерфейс стоит, чтобы его немного освоить.
GNU/Octave как иллюстрированное пособие по курсу линейной алгебры
Если вас учили или учат в институте старые советские преподаватели по старым советским книжкам, то GNU/Octave вам сильно поможет понять линейную алгебру, без которой инженеру абсолютно нечего делать в повседневной деятельности.
Кстати, вместо старых советских учебников лучше купить \ найти на просторах Интернета замечательную книжку Linear Algebra and Its Applications за авторством Gilbert Strang. Ещё лучше вместе с книжкой посмотреть его видеолекции, чтобы сэкономить время, если требуется освежить разделы линейной алгебры.
Также автор этих строк настоятельно рекомендует купить \ достать превосходный, умопомрачительно подробный Handbook of Linear Algebra авторства несравненной Leslie Hogben. Эти 1400 страниц плотного математического справочника содержат все факты о линейной алгебре, которые вам могут когда-либо пригодиться в студенческой и научной жизни.
Вооружившись свежими книгами, смело идём постигать линейную алгебру до полного просветления.
Курс молодого бойца Линейной Алгебры
Для разбега посмотрим на набор матриц:
A=[1 2; 4 5 ]
A =
1 2
4 5
B = [1, 1; 1, 1]
B =
1 1
1 1
Столбцы матрицы можно набирать пробелом или запятой, разделение на строки - точка с запятой ;
Как нас учит линейная алгебра, матрицы можно
складывать
octave:3> A+B
ans =
2 3
5 6
вычитать
octave:4> A-B
ans =
0 1
3 4
и умножать друг на друга, если они подходят по размерностям:
octave:5> A*B
ans =
3 3
9 9
Делить матрицы друг на друга, как числа, нельзя, но можно умножить матрицу на инверсную. Octave, как и MATLAB, это знают, но пользователь об этом может не догадываться:
octave:> [1 2; 3 4]/[1 1; 1 1]
ans =
0.75000 0.75000
1.75000 1.75000
Такая операция приводит к умножению матрицы A на (псевдо)инверсную матрицу B:
octave:10> [1 2; 3 4]*pinv([1 1; 1 1])
ans =
0.75000 0.75000
1.75000 1.75000
То есть будет вычислено Least Squares решение, как намекает нам документация. Пойдём дальше и посмотрим на другие возможности Octave.
Системы линейных уравнений
На семинарах по линейной алгебре пытаются учить решению систем линейных уравнений, которые выглядят несколько устрашающе:
Эту систему можно переписать в компактном виде А*X = В где коэффициенты являются элементами матриц:
Для Октавы это будет две команды:
octave:9> A=[1 3 5; 3 1 3; 4 1 3]
A =
1 3 5
3 1 3
4 1 3
и
octave:10> B = [22;14;15]
B =
22
14
15
Решать системы уравнений можно по-разному, например так:
octave:11> A^(-1)*B
ans =
1
2
3
Но это в реальных задачах всегда стараются избегать такого решения. Часто бывает так, что уравнений больше, чем неизвестных - тут нам на помощь придёт метод наименьших квадратов (Least Squares). В Октаве и Матлабе решение в смысле least squares можно записать компактно:
octave:12> A\B
ans =
1
2
3
Это на самом деле (A^T * A)^(-1)*A^T * B или, в выражениях Октавы, inv(A'*A)*A'*B
Это ещё один популярный сорт рыбьего жира, коим пичкают скубентов злые преподаватели высших учебных заведений, почти никогда не поясняя, зачем они (собственные вектора и значения) нужны. А они нужны, и даже очень - в обработке сигналов и изображений, для алгоритмов Face Detection и для анализа стабильности контроллеров в теории (и практике!) управления, и для много чего ещё.
В Octave/MATLAB вычислением оных собственных векторов и значений занимается команда eig и сейчас мы её пощупаем. Вводим матрицу
octave:13> A=[1 3 5; 3 1 3; 4 1 3]
A =
1 3 5
3 1 3
4 1 3
теперь считаем собственные вектора U и значения V вот так:
octave:15> [U,V] = eig(A)
U =
-0.62701 -0.82511 -0.22384
-0.51095 0.23555 -0.81183
-0.58804 0.51353 0.53928
V =
8.13398 0.00000 0.00000
0.00000 -2.96831 0.00000
0.00000 0.00000 -0.16567
Матрица выдаётся V в канонической форме, с собственными значениями по главной диагонали. Этим примером хотелось показать eigenvalue decomposition в действии:
[U,V] = eig(A);
и обратно:
U*V*inv(U)
получится опять А.
Отмечу, что Octave/MATLAB считают eigenvalue decomposition совсем не так, как вас учат в институте, поэтому знаки собственных значений могут отличаться от посчитанных вами. Матлабовская документация намекает на причины этого.
Едва ли в курсе линейной алгебре вам расскажут, как посчитать собственные вектора для матриц размерности более 3 или 4. Хотя метод iterative QR decomposition прекрасно реализован в Octave и умеет это делать. Книги Gilbert "наше линейное всё" Strang ждут своих заинтересованных читателей, коим откроется это и многое другое.
Эти важные свойства матриц, как правило, довольно просто посчитать вручную, но если это делать лень, можно запрячь Octave:
octave:16> det(A)
ans = 4
и ранг матрицы:
octave:17> rank(A)
ans = 3
На Октаве можно решать и другие задачи из курса алгебры.
Продвинутое использование GNU/Octave
Несколько примеров, приведённых ниже, используются уже для написания программ на Octave/MATLAB, а не просто для того, чтобы посчитать домашнее задание.
Иногда удобнее всего работать с матрицей, если вытянуть её в одну строчку. Потом обычно её нужно собрать обратно, после того, как над ней сделали что-то. Для этого нам пригодится команда reshape.
Вот например:
>> x = [1 2 3 4 5 6 ]
x =
1 2 3 4 5 6
Мы хотим сделать этот вектор-строку в виде матрицы 2х3 - легко:
>> x1 = reshape(x,2,3)
x1 =
1 3 5
2 4 6
И обратно собрать:
>> x1 = reshape(x,1,6)
x1 =
1 2 3 4 5 6
Разреженые (Sparce) Матрицы
Иногда встречаются матрицы, в которых очень много нулей и очень мало ненулевых значений. Памяти занимают много, считаются долго. Для экономии ресурсов нам на помощь спешит Sparce Matrix.
Используя специально предназначенные алгоритмы для работы с разреженными матрицами, можно сильно сэкономить память и ускорить вычисления.
Например:
>> a = [1,0,0;0,2,0;0,0,3]
a =
1 0 0
0 2 0
0 0 3
Нулей в матрице много, а значений - всего два. Сделаем её разреженной:
octave:19> a_sparse = sparse(a)
a_sparse =
Compressed Column Sparse (rows = 3, cols = 3, nnz = 3)
(1, 1) -> 1
(2, 2) -> 2
(3, 3) -> 3
Отлично. Теперь, например, мы хотим выцедить из неё главную диагональ. Для этого заведём переменную:
>> d = [0]
d =
0
и воспользуемся специальной командой для разреженных матриц:
>> a_diag = spdiags(a_sparse,d)
a_diag =
1
2
3
Здесь d содержит номера диагоналей, которые надо вытащить: 0 - главная диагональ, 3 - третья справа от главной (выше на 3 позиции), а -2 это под главной диагональю на 2 позиции.
Помимо матриц, в Octave можно хранить ещё и структуры. Структура это удобный метод хранения различных типов данных в одной "переменной".
Например, в симуляторе есть данные, касающиеся параметров турбулентности атмосферы, и они все хранятся в одной структуре по имени atm.
Создание структуры дело нехитрое, и это можно делать в цикле:
for ii=1:4
atm.layer_height{ii} = height;
end
Для просмотра содержимого структуры достаточно вызвать её по имени.
>> atm
atm =
n_layers: 1
layer_height: {[5000]}
layer_thickness: {[100]}
Cn_squared: {[1.3514e-17]}
Cn_squared_model: 'pureHufnagel'
psi_cell: {[128x128 double]}
nx_grid_points: {[128]}
ny_grid_points: {[128]}
screen_width: {[16]}
outer_scale: {[1.9512]}
inner_scale: {[0.0021]}
sampling_delta: {[0.1250]}
sampling_delta_f: {[0.0625]}
r0: 0.1600
power_spectrum_model: 'kolmogorov'
phase_screenwidth: 16
Reynolds_number: 9000
Теперь, скажем, я хочу передать значение n_layers в цикл (это число слоёв турбулентной атмосферы). Пишем:
k = atm.n_layers
Но это просто число. Так как здесь используются слои, структура получается многомерной. Например, нужно получить высоту слоя турбулентности layer_height пишем:
>> k = atm.layer_height(1)
получаем:
k =
[5000]
Это первый элемент структуры, но он не просто число, а cell array:
>> whos k
Name Size Bytes Class
k 1x1 68 cell array
Grand total is 2 elements using 68 bytes
Что делать, как спрашивают классики? Фигурные скобки позволяют получить непосредственно значение элемента:
>> k = atm.layer_height{1}
k =
5000
Теперь это число и с ним можно работать.
>> whos k
Name Size Bytes Class
k 1x1 8 double array
Удобство структур в том, что их можно передавать в функции, как одну большую переменную. Если при этом вы захотите добавить новые переменные, корректировать вызов функций не придётся - вы передаёте всю структуру целиком, так что все необходимые переменные там будут.
Ссылки
На этот пост меня сподвиг Блог ни о чем и его заметки про Октаву. Из оных заметок может сложиться впечатление, что Октава это "типа калькулятор, только консольный". Что неверно: несмотря на прорву недостатков Октавы (обрывочную документацию, криво реализованные матлабовские функции, неспособность выдавать интерактивные графики и зачаточный графический интерфейс) это - вполне себе мощная система численных расчётов и язык программирования. В качестве пособия по линейной алгебре GNU/Octave более чем достаточна.