Что такое шифрование? У этого термина есть много определений. Одни подробные и сложные, другие попроще. Но можно просто сказать, что шифрование - это способ преобразования пригодного для чтения текста, делающий невозможным его прочтение третьими лицами, причем текст снова становится пригодным для чтения после верификации ключа. Криптография возникла задолго до компьютерной эры. Хотя растущая производительность компьютеров позволяет создавать более совершенные и надежные шифры, а криптография стала неразрывно связана с информационными технологиями, история шифровального дела насчитывает не одну тысячу лет. Прежде чем перейти к обсуждению современной криптографии, я хотел бы остановиться на нескольких давно известных методах шифрования.
Шифры в давние времена
Шифр Цезаря
Это один из наиболее древних известных шифров, которым, как можно предположить исходя из его названия, пользовался римский император Юлий Цезарь. Шифр применялся для защиты важных сообщений, передаваемых через связных, чтобы не позволить врагу обнаружить армию в случае перехвата сообщения. Суть шифра состоит в замене каждой буквы на букву, отстоящую от нее в алфавите на 3 позиции вправо. Подобные шифры, основанные на замене одних букв другими, называются подстановочными. Моноалфавитные шифры (к которым относится и шифр Цезаря) - это разновидность подстановочных шифров, в которой каждой букве нешифрованного текста всегда соответствует одна и та же буква в шифрованном тексте.
Открыть в полный размер' href="http://www.securelist.com/ru/analysis/208050597/images/vlill/maciej_encryption_de_pic3.png" target=_blank style=color:white;>Открыть в полный размер' href="http://www.securelist.com/ru/analysis/208050597/images/vlill/maciej_encryption_de_pic3.png" target=_blank>
ROT13
Это шифр, в котором каждая буква заменяется на отстоящую от нее в алфавите на 13 позиций вправо. Это очень простой шифр, не дающий никакой реальной безопасности. В наши дни подобные методы шифрования используются для курьеза или для шифрования информации, не представляющей особенной ценности. Этот метод шифрования не различает прописные и строчные буквы. Из приведенного ниже примера видно, что механизм шифрования в данном случае ничем не отличается от применяемого в шифре Цезаря: единственное различие состоит в величине сдвига.
![]()

ADFGVX
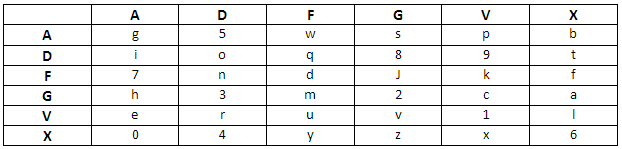
Этот шифр, представляющий собой усовершенствованный вариант более раннего шифра ADFGX, использовали в Германии во время Первой мировой войны для шифрования команд и распоряжений. Алгоритм состоит в сопоставлении пары букв (используются только буквы A, D, F, G, V и X) каждой букве шифруемого текста. Чтобы затруднить криптографический анализ, используется ключевое слово и таблица, заполненная буквами и цифрами. В распоряжении адресата зашифрованного сообщения должны быть как ключевое слово, так и цифро-буквенная таблица. Пример такой таблицы приведен на следующем рисунке:
Предположим, что нужно зашифровать слово Kaspersky. Для этого необходимо сначала получить пары букв, соответствующие буквам шифруемого слова, с помощью приведенной выше таблицы ADFGVX:
K - FV
A - GX
S - AG
P - AV
E - VA
R - VD
S - AG
K - FV
Y - XF
Следующий шаг - выбор пароля. Остановимся на слове SZYFR (ШИФР по-польски). Далее последовательно вводим пары букв, полученные при шифровании слова Kaspersky из таблицы ADFGVX, в новую таблицу. В каждом столбце должно быть одинаковое количество букв, и если для заполнения таблицы имеющихся букв не хватает, то надо их добавить. В данном случае двум последним буквам в таблице соответствует число 0.
Последний шаг - расстановка столбцов, начинающихся с букв ключевого слова, в алфавитном порядке.
Теперь из последней таблицы записывается зашифрованное слово. Для этого записываем буквы из таблицы слева направо. Чтобы усложнить задачу расшифровки, в полученную последовательность после каждой шестой буквы вставляется пробел.


Одноразовый блокнот
Этот шифр, созданный в 1917 году Гильбертом Вернамом, очень надежен, поскольку методов его взлома не существует (в частности, неприменим метод прямого подбора, основанный на переборе всех возможных сочетаний символов для определения их правильного порядка). Существуют две версии этого шифра: на основе двоичного ключа и стандартного (буквенного) ключа. Они различаются способом шифрования текста: первая использует алгоритм объединения шифруемого текста с ключом при помощи операции "исключающее ИЛИ" (XOR), вторая - алгоритм Виженера. Ключ обладает высочайшей эффективностью благодаря своей длине (которая совпадает с длиной самого сообщения), тому, что он представляет собой случайную последовательность, и тому, что он используется только один раз. Ответ отправителю генерируется с помощью нового ключа. Несмотря на то, что оба алгоритма ("исключающее ИЛИ" и алгоритм Виженера) по сути являются подстановочными шифрами, при выполнении трех упомянутых условий (длина ключа, его случайность и одноразовость) этот метод шифрования обладает абсолютной криптостойкостью. В приведенном ниже примере я рассмотрю двоичный метод, то есть алгоритм, основанный на использовании логического оператора "исключающее ИЛИ" (XOR).
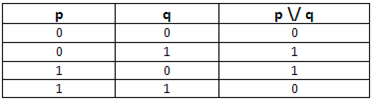
Операция XOR называется также разделительной дизъюнкцией. Если из операндов p и q один (но не оба) является истинным (т.е. имеет значение 1), то выражение p XOR q также истинно. В противном случае оно ложно.
Чтобы зашифровать сообщение "Kaspersky", нужно сначала записать его в двоичной системе. На практике, конечно, сообщение (например, письмо) будет длиннее, а значит, лучше защищено, поскольку длина ключа всегда равна длине сообщения.
Записав сообщение в двоичной системе, нужно создать пароль. При этом важно, чтобы пароль был сгенерирован совершенно случайным образом, а это непростая задача. Хотя существует множество генераторов псевдослучайных чисел, даже из их названия следует, что они не гарантируют полной случайности, а значит, возможно обнаружение определенных закономерностей (периодичности). Лучшим решением этой проблемы был бы генератор, использующий, к примеру, случайный характер и изменчивость величин температуры компьютерных компонентов (например, процессора). Чтобы проиллюстрировать процесс шифрования, основанный на данном методе, были сгенерированы следующие числа:
Следующий шаг - выполнение операции разделительной дизъюнкции (XOR):
Будучи зашифрованным, наше сообщение примет следующий вид:
Поскольку созданный пароль используется только один раз, составляющие его числа случайны, а его длина совпадает с длиной шифруемого сообщения, данный вид шифрования известен как шифрование OTP (от английского One-Time Password - одноразовый пароль), поскольку пароль используется лишь один раз и после этого становится бесполезным. Пытаться взломать пароль бессмысленно, потому что без ключа воссоздать исходное сообщение невозможно, ведь последовательность символов в зашифрованном тексте случайна в той же степени, в какой и последовательность символов в ключе. Зная результат разделительной дизъюнкции, можно пытаться по одному заменять символы и вычислять пароль на основе получившейся комбинации. Но если мы не знаем, правильно ли произведена замена, пароль нам выяснить не удастся - тем более, что он использован лишь однажды. Поэтому криптоанализ, основанный на частоте, с которой встречаются определенные символы или сочетания символов (как в подстановочных шифрах), невозможен - ведь эта характеристика будет меняться от одного сообщения к другому.
Современные алгоритмы
Перейдем к обсуждению алгоритмов, применяемых в наши дни. Прежде всего, необходимо объяснить разницу между симметричным и асимметричным шифрованием. Далее будут кратко описаны алгоритмы AES и RSA, причем второй более подробно и с привлечением примера.
Симметричное шифрование
Название этого типа шифрования объясняется тем, что в большинстве симметричных шифров сообщение шифруется и расшифровывается одним и тем же ключом. Внутри этой группы шифры подразделяются на блочные и потоковые. В блочных шифрах перед шифрованием сообщения разбиваются на блоки данных, а потоковые шифры преобразуют каждый бит сообщения в соответствии с определенным алгоритмом. Проблему может представлять передача ключа, поскольку без него адресат не сможет расшифровать сообщение. Таким образом, надежность симметричного шифра зависит прежде всего от ключа.
AES (англ. Advanced Encryption Standard - прогрессивный стандарт шифрования) - широко распространенный симметричный алгоритм шифрования. Он стал победителем конкурса, объявленного с целью найти замену устаревшему стандарту DES (англ. Data Encryption Standard - стандарт шифрования данных), который не обеспечивал необходимого уровня защиты данных. Алгоритм AES использует 128-, 196- и 256-разрядные ключи. Он шифрует блоки данных различной длины, что, в сочетании с различной длиной ключей, обеспечивает очень высокий уровень защиты от взлома.
Асимметричное шифрование
Этот вид шифрования в наши дни очень распространен: электронные цифровые подписи - лишь один из примеров его применения. В процессе шифрования текста создается пара ключей - секретный (частный) и открытый (публичный). Секретный ключ предназначается для создания цифровой подписи подтверждающей подлинность сообщений. Открытый ключ является общедоступным и позволяет каждому получателю сообщения убедиться, что полученное сообщение не подверглось изменению при пересылке.
Для шифрования сообщений, напротив, применяется открытый ключ, а для их расшифровки необходим частный ключ.
Я опишу работу современного алгоритма шифрования на примере RSA. Выше я не писал об этом алгоритме, потому что хочу остановиться на нем более подробно и рассмотреть пример текста, зашифрованного с его помощью.
RSA известен также как алгоритм Ривеста, Шамира и Адлемана (Rivest, Shamir and Adleman), чьи инициалы и образуют сокращение RSA. Это первый алгоритм, основанный на описанном выше методе асимметричного шифрования, и он часто используется для создания электронных цифровых подписей. Три создателя алгоритма пытались на практике реализовать предложенную Диффи (Diffie) и Хеллманом (Hellman) концепцию применения секретных и открытых ключей для шифрования данных. После нескольких модификаций идея предоставления одного ключа всем пользователям и расшифровки текста с помощью второго ключа была, наконец, реализована на практике.
Прежде чем рассмотреть практический пример шифрования текста с помощью алгоритма RSA, остановимся на смысле входящих в формулы символов.
p - первое большое простое число
q - второе большое простое число
(простые числа - это целые числа, которые делятся без остатка только на себя и на единицу)
n - произведение больших простых чисел p и q (при 256-разрядном шифровании число цифр n превышает 300)
m - сообщение, записанное в виде числа
e - ключ, применяемый при шифровании, представляющий собой такое целое число, взаимно простое с произведением (p-1)(q-1), что e < n (у взаимно простых чисел наибольший общий делитель равен 1).
Секретный (дешифровочный) ключ - пара чисел d и n, где
d
рассчитывается по следующей формуле:
ed = 1 (mod (p-1)(q-1))
Открытый ключ - пара чисел n and e
Шифрование:
c = me (mod n)
Дешифрование:
m = cd (mod n)
Далее мы рассмотрим процесс шифрования. Известно, что для этого требуются большие простые числа. Но, чтобы сделать процесс более наглядным, я использую небольшие простые числа. Они слишком малы для обеспечения достаточной криптостойкости алгоритма, но с ними проще выполнять необходимые вычисления.
Предположим, мы хотим зашифровать букву Y (расчеты для слов и целых предложений потребуют слишком много места, поэтому мы ограничимся одной буквой). В десятичной системе счисления букве Y соответствует число 89. Теперь у нас есть сообщение, записанное в виде числа, т.е. m. Далее необходимо выбрать простые числа p и q. Поскольку числа 19 и 29 делятся только на себя и 1, они являются простыми (надо только помнить, что при "реальном" шифровании эти числа должны быть гораздо больше). Кроме того, надо выбрать число e, взаимно простое с произведением (p-1)(q-1). Теперь приступим к расчетам:
n = p * q
n = 551
(p-1)*(q-1) = 504
e = 5
Это взаимно простые числа, поскольку у 5 и 504 наибольший общий делитель равен 1 (требование e < n также выполнено).
Теперь у нас есть все необходимые данные для того, чтобы приступить к шифрованию. В процессе вычислений необходимо также рассчитать d.
m = 89
c = me (mod n)
c=895 (mod 551)
c = 5584059449 (mod 551)
c = 90
После шифрования наше сообщение "Y" имеет значение 90. Для того чтобы расшифровать его, необходимо использовать секретный ключ. Но прежде, как говорилось ранее, необходимо вычислить значение d.
ed = 1 (mod (p-1)*(q-1))
5d = 1 (mod 504)
5d = 505
d = 505/5
d = 101
Чтобы расшифровать сообщение, выполняются следующие вычисления:
c = 90
m = cd (mod n)
m = 90101 (mod 551)
m = 89
Число 89 соответствует символу Y. Это значит, что сообщение зашифровано и расшифровано верно. Поскольку в реальности подобные операции выполняются над числами, значительно большими, чем использованные в примере, применение этого алгоритма обеспечивает гораздо более высокий уровень защиты. Отметим, что каждый алгоритм имеет свои слабые места и рано или поздно поддается взлому. Это лишь дело времени, поскольку мощность вычислительных систем постоянно растет. Слабость алгоритма состоит в возможности нахождения секретного ключа методом факторизации (к счастью, факторизация - сложная задача, требующая слишком много времени для того, чтобы быть применимой на практике).
Факторизация - это разложение больших целых чисел на множители. Чтобы прояснить смысл факторизации, приведу пример. Пусть x - наше большое целое число. После разложения на множители получим множители y1, y2, y3, yn. Таким образом, x=y1 y2 y3 yn.
Чтобы найти секретный ключ, необходимо разложить на множители число n, входящее в открытый ключ, и таким образом определить простые числа p и q. В случае успешного решения этой задачи сообщение было бы чрезвычайно легко расшифровать. К счастью, надежность шифров RSA обеспечивается тем, что факторизация очень больших чисел, используемых в наше время, - очень сложный процесс, требующий больших временных затрат. Несмотря на то что существуют алгоритмы, позволяющие ускорить процесс факторизации, время, необходимое на его осуществление, все еще очень велико. В наши дни применяются ключи длиной более 1024 бит. При этом наибольшая длина когда-либо взломанного ключа RSA составляет 663 бита. Реальной угрозой и, возможно, даже приговором алгоритму RSA станут квантовые компьютеры. Как можно понять из названия, их работа основана на принципах квантовой механики, а их быстродействие будет значительно превышать скорость работы традиционных компьютеров. В результате время, необходимое для разложения больших чисел на простые множители, будет существенно меньшим, чем сейчас. Таким образом мы придем к квантовой криптографии… Но надо помнить, что шифрование - это своеобразная гонка вооружений. Пока алгоритм обеспечивает необходимый уровень защиты, невозможно предугадать, сколько он еще продержится. Рано или поздно кто-то найдет способ взломать его.
Шифровать или не шифровать...
Многие пользователи не понимают, насколько ценны данные на их компьютерах и сменных дисках. Я имею в виду не музыкальные файлы и фотографии (хотя киберпреступники могут использовать их, в частности в целях шантажа), а данные и пароли, сохраненные в браузерах и интернет-пейджерах, сообщения электронной почты, находящиеся на жестком диске, а также статьи и другая информация, не подлежащая разглашению. Когда вы продаете свой компьютер или жесткий диск, просто отформатировать диск недостаточно. Всю информацию на нем будет возможно восстановить, причем даже с помощью бесплатных программ. Нет необходимости придумывать сценарии использования собранных данных - достаточно представить себе, что в распоряжение третьих лиц попали реквизиты кредитной карты или письмо с конфиденциальными данными компании. Если собрать достаточное количество личных данных, возможно и "подменить" человека, создав его фальшивого двойника.
Известны случаи, когда злоумышленники покупали подержанные жесткие диски на интернет-аукционах с единственной целью - восстановить удаленные данные и с их помощью шантажировать предыдущих владельцев. К сожалению, некоторые из жертв идут на поводу у шантажистов и платят выкуп, чтобы избежать раскрытия личной или корпоративной информации.
Один из способов предотвратить подобное развитие событий - шифровать данные на диске. Шифровать можно отдельные файлы, разделы и жесткие диски целиком. Некоторые программы позволяют создавать зашифрованные разделы на диске, доступ к которым невозможен без пароля или ключа. Подобное решение делает перемещение важных документов с одного компьютера на другой более безопасным. Достаточно перенести файл в зашифрованный раздел на диске A, затем поместить весь раздел на сменный диск и подключить его к компьютеру B. Даже если сменный диск будет потерян или украден, ущерб не будет столь значительным (он зависит от примененного алгоритма шифрования), а времени на реагирование и защиту от последствий потери данных будет больше.
Чтобы показать, что шифровать свои данные несложно и под силу любому, я подготовил три коротких видеоролика на английском языке. В них демонстрируется процесс шифрования данных с помощью бесплатной утилиты TrueCrypt:
- Creating an encrypted file warehouse
- Securing the volume with an additional key
- Using removable disks as encrypted disks
Подобные решения были бы особенно полезны организациям, которые хранят личные данные пользователей. К сожалению, последнее время все чаще приходится слышать о краже и потере CD и жестких дисков, содержащих личные данные. Эти случаи не были бы столь неприятными, если бы данные на носителях были защищены криптостойкими алгоритмами.
- В 2007 году в Великобритании были потеряны хранившиеся на незащищенных компакт-дисках персональные данные 25 миллионов граждан: номера банковских счетов, даты рождения, адреса, имена и фамилии, номера в национальной системе социального страхования.
- Всего лишь месяцем позже произошел другой инцидент, также имеющий отношение к Великобритании. В штате Айова (США) был потерян жесткий диск, содержащий данные о трех миллионах британских кандидатов на получение водительских прав. Британское агентство, отвечающее за проведение экзаменов по вождению, поручило хранение персональных данных кандидатов в водители американской компании-подрядчику. Однако носитель с данными подрядчик так и не получил, и информацию до сих пор не удалось восстановить.
К сожалению, подобные ситуации возникают все чаще, и шифрование столь важной информации, несомненно, помогло бы решить проблему. Джереми Кларксон, британский ведущий автомобильной телепрограммы Top Gear, - один из тех, кто на своем опыте убедился в том, как легко поддаться ложному чувству безопасности, рассуждая так: "Для чего вообще могут сгодиться мои данные?" . В одной из своих передач он сказал, что такие данные никому не нужны, и решил опубликовать свои банковские реквизиты и информацию, необходимую для осуществления банковских переводов. Спустя совсем короткое время с его счета пропали 500 фунтов стерлингов. После этого инцидента он сказал: "Банк не может выяснить, кто это сделал… и они не могут помешать сделать это снова. Я был неправ, и я наказан за свою ошибку". (http://news.bbc.co.uk/2/hi/entertainment/7174760.stm)
Этот случай доказывает, как важно защищать личные данные путем шифрования. Мы не можем влиять на то, как хранят данные частные компании и государственные организации, но безопасность наших собственных данных целиком в наших руках.
Но иногда шифрование данных применяется совсем в иных целях, чем те, что я описал выше. Те же методы, что разработаны для защиты наших данных от несанкционированного доступа, могут быть использованы и для того, чтобы полностью заблокировать нам доступ к собственным файлам. В 2006 году в Сети появился вирус под названием Gpcode. Он зашифровывал файлы более 80 типов на компьютерах жертв, а затем требовал заплатить за их расшифровку.
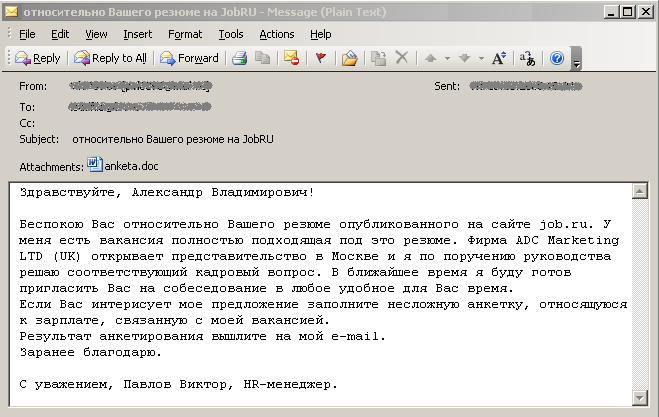
Вирус распространялся по электронной почте. Жертвы получали письмо следующего содержания:
Нетрудно догадаться, что вложение содержало троянскую программу, которая и загружала сам вирус. Среди прочих, Gpcode шифровал файлы следующих типов: PDF, DOC, HTML и RAR. Все вредоносные программы, загруженные и установленные при открытии сообщения, удалялись. Оставалось только следующее сообщение:
Some files are coded by RSA method.
To buy decoder mail: k47674@mail.ru
with subject: REPLY
Поначалу вирус использовал очень слабые и далекие от совершенства алгоритмы шифрования с 56-битным ключом. Но автор постепенно совершенствовал свое творение, в конце концов сумев создать ключ RSA длиной 660 бит. Несмотря на то что подобные ключи обеспечивают чрезвычайно высокий уровень защиты, а наибольшая длина когда-либо взломанного ключа составляла 663 бита, специалистам "Лаборатории Касперского" удалось (основываясь на допущенных автором GPcode ошибках) создать эффективный метод расшифровки в тот же день, когда вирус был обнаружен.
Необходимо помнить, что шифрование - обоюдоострое оружие. В зависимости от того, кто и как его применяет, оно может быть причиной серьезного ущерба или надежным средством защиты. С одной стороны, шифрование способствует свободе слова, поскольку зашифрованные сообщения невозможно прочитать без пароля, а с другой, оно несет угрозу национальной безопасности. Ведь если шифрование доступно всем, то преступные организации могут скрывать с его помощью информацию. Но не следует поддаваться паранойе. Важно с умом использовать свои знания для защиты собственных данных - за нас этого никто не сделает.