Надстройка MS Excel "Поиск решений" позволяет решать широкий круг задач на оптимизацию. Думаю, многие посетители сайта изучали в институте линейное программирование или исследования операций. "Поиск решений" в Excel позволяет в считанные секунды находить оптимальные решения достаточно сложных моделей, кстати не только линейных, без знания алгоритмов и длительных рутинных итерраций.
Оптимизационные модели широко используются в экономике и технике. Среди них задачи подбора сбалансированного рациона питания, оптимизации ассортимента продукции, транспортная задача и пр., и пр.
Модели всех задач на оптимизацию состоят из следующих элементов:
1. Переменные - неизвестные величины, которые нужно найти при решении задачи.
2. Целевая функция - величина, которая зависит от переменных и является целью, ключевым показателем эффективности или оптимальности модели.
3. Ограничения - условия, которым должны удовлетворять переменные.
Поиск решения такой модели рассмотрим на примере вопроса, поступившего на форум. Итак, сам вопрос:
Издательский дом "Геоцентр-Медиа" издаст два журнала: "Автомеханик" и "Инструмент", которые печатаются в трех типографиях: "Алмаз-Пресс", "Карелия-Принт" и "Hansaprint" (Финляндия), где общее количество часов, отведенное для печати и производительность печати одной тысячи экземпляров ограничены и представлены в следующей таблице:
Спрос на журнал "Автомеханик" составляет 12 тысяч экземпляров, а на журнал "Инструмент" -не более 7,5 тысячи в месяц.
Определите оптимальное количество издаваемых журналов, которое обеспечит максимально выручку от продажи.
Давайте разберемся, что здесь является переменными, что целевой функцией, что ограничениями.
Найти нам необходимо оптимальное количество издаваемых журналов каждого вида. А издавать их можно в трех типографиях на разных условиях. Вот и получается, что нам необходимо определить размер тиража каждого журнала напечатанного в каждой типографии. Это и будут наши переменные.
По какому принципу их подбирать, что считать эффективным, что нет. Перед нами поставлена задача получить максимальную выручку. Таким образом, цель - максимальная выручка.
Теперь ограничения. В условиях сказано, что каждая типография может выделить на наш тираж только определенное время. Длительность печати тысячи единиц тиража каждого журнала каждой типографией известна.
Таким образом, произведение объема тиража на длительность печати тысячи единиц для каждой типографии не может быть больше заданного количества времени.
Еще одно важное ограничение, о котором обычно забывают - переменные должны быть неотрицательными.
Попытаемся представить модель в Excel.
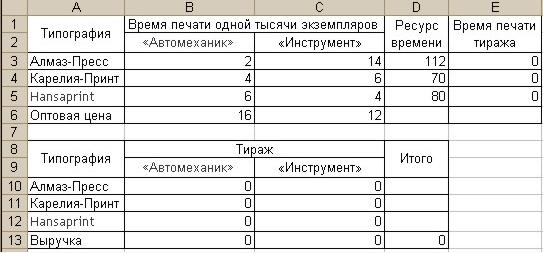
Переменные, то есть объем тиража, находятся в ячейках B10:C12. Целевая функция - в ячейке D13. Обратите внимание, целевая функция построена формулой, ссылаясь на ячейки с переменными и исходные данные (стоимость единицы тиража).
Также формулами подсчитывается фактическое время печати тиража в каждой из типографий (ячейки E3:E5).
Все готово, приступаем решению задачи с помощью надстройки.
Включается она через меню Сервис - Поиск решений. Если такого пункта меню нет, войдите в меню Сервис - Надстройки и отметьте галочкой соответствующую надстройку. Может понадобиться установочный комплект Office.
Перед Вами появится следующий диалог:
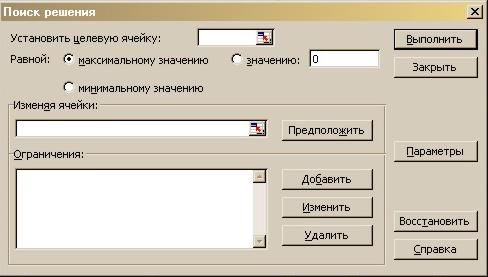
Здесь указываем адрес целевой ячейки, отмечаем, что ее нужно привести к максимальному значению, изменяя ячейки $B$10:$C$12. Диапазоны можно указывать мышью - станьте в нужное поле диалога и выделите на листе нужные ячейки. Адрес автоматически попадет в диалог.
Добавляем ограничения. После нажатия кнопки Добавить появляется диалог:
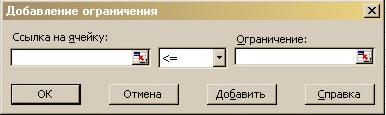
Вспоминаем. У нас фактическое время печати тиража в каждой типографии не может превышать заданного лимита.
Для Алмаз-Пресс ограничение будет таким E3 <= D3. В ячейке E3 должна быть формула суммы продолжительности печати тиража первого и вторго журналов в этой типографии, полученной перемножением тиража на норму времени.
Думаю, понятно, как ввести в диалог описанное ограничение.
Если нажать Ок, ограничение будет добавлено, а диалог закроется. Чтобы несколько раз не открывать диалог, сделана кнопка Добавить. Ограничение сохраняется, а диалог очищается для добавления следующего ограничения. Аналогично добавляем ограничения для оставшихся типографий.
Ограничения неотрицательности можно также задать с помощью этого диалога - для каждой ячейки с объемом тиража установить ограничение >=0.
Но учитывая, что такие ограничения встречаются в задачах на оптимизацию слишком часто, разработчики надстройки предусмотрели возможность быстрой установки ограничения неотрицательности для всех переменных модели. Нажимаем Ok, возвращаемся в первый диалог и нажимаем кнопку Параметры.
Здесь достаточно отметить галочку Неотрицательные значения.
Все модель готова к расчету:
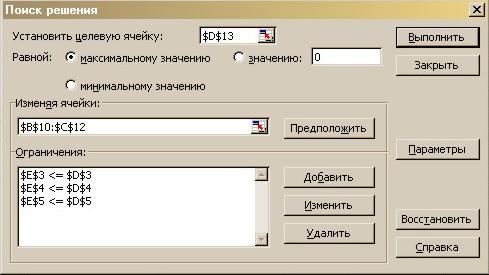
Нажимаем Выполнить.
Через пару секунд Вы будете иметь оптимальное решение.
Теперь выберите Сохранить решение и нажмите Ok.
Можете проверить решение, пробуя подставлять другие значения тиража, перераспределяя тираж между типографиями. Вряд ли Вам удастся улучшить результат.
Конечно, результат не стопроцентный. Бывают слишком сложные модели, модели совсем не имеющие решений (модели с несходимыми ограничениями). Кроме того, если Вы обратили внимание, в параметрах модели можно задать максимальное время решения, число итерраций, точность и другие установки. Но это для профессионалов.
Что радует, все настройки модели (целевая ячейка, область переменных, ограничения, параметры) сохраняются в книге и при изменении исходных данных их не нужно вводить заново. Достаточно открыть надстройку и запустить повторный поиск решения.
