Для того, чтобы вращать объекты (или камеру), необходима серьезная математическая база, с помощью которой будут расчитываться координаты всех объектов при выводе на "плоский" экран компьютера. Сразу хочу сказать, что не стоит пугаться, все математические библиотеки уже написаны за нас, мы будем их только использовать. В любом случае, следующий текст пропускать не нужно, независимо от уровня знаний математики.
1. Матрицы, общие понятия
Что такое матрицы? Вспоминаем высшую математику: матрица ¬- это набор чисел с заранее известной размерностью строк и столбцов.
Матрицы можно складывать, умножать на число, перемножать друг с другом и много еще чего интересного, но этот момент мы пропустим, т.к. он достаточно подробно изложен в любом учебнике по высшей математике (учебники можно поискать на google.com). Мы будем пользоваться матрицами как программисты, мы их заполняем и говорим, что с ними делать, все расчеты произведет математическая библиотека Direct3D, поэтому нужно включить в проект заголовочный модуль d3dx9.h (и библиотеку d3dx9.lib).
Наша задача - создать объект, т.е. заполнить матрицу координатами вершин объекта. Каждая вершина - это вектор (X, Y, Z) в трехмерном пространстве. Теперь, чтобы произвести какое-то действие, нужно взять наш объект (то есть матрицу) и умножить на матрицу преобразования, результат этой операции - новый объект, заданный в виде матрицы.
В Direct3D определены и используются три основные матрицы: мировая матрица, матрица вида и матрица проекции. Рассмотрим их подробнее.
Мировая матрица (World Matrix) - позволяет производить вращение, трансформацию и масштабирование объекта, а также наделяет каждый из объектов своей локальной системой координат.
Функции для работы с мировой матрицей:
Матрица вида (View Matrix) - определяет местоположение камеры просмотра сцены и может состоять из любых комбинаций трансляции и вращения.
D3DXMatrixLookAtLH()и D3DXMatrixLookAtRH() определяет положение камеры и угла просмотра для левостороней и правостороней систем координат соответственно.
Матрица проекции (Projection Matrix) - создает проекцию 3D сцены на экран монитора. С ее помощью объект трансформируется, начало координат переносится в переднюю часть, а также определяется передняя и задняя плоскости отсечения.
Заполняя эти матрицы и делая преобразования, вы создаете трехмерную сцену, в которой получаете возможность перемещать, вращать, приближать, удалять и производить другие действия над объектами, в зависимости от ваших потребностей.
2. Создание объекта
Создаем новый проект, аналогично первому. Прежде чем продолжить усложнять наш код, разобьем его на части для лучшей читаемости кода. Наш проект логично разделить на три составляющие:- Окно Windows (инициализация окна, сообщения, …)
- Инициализация 3D (загрузка координат объектов, удаление ресурсов, …)
- Рендер сцены (матрицы, рисование примитивов, …)
Добавляем заголовочный файл и библиотеку для использования матричных функций
#include <d3dx9.h> // или C:\DXSDK\Include\d3dx9.h #pragma comment(lib, "d3dx9.lib") //или C:\\DXSDK\\Lib\\d3dx9.lib
Также нам понадобятся стандартные функции работы со временем, поэтому подключаем соответствующий заголовочный файл:
#include <mmsystem.h>
Изменим формат представления вершин:
#define D3DFVF_CUSTOMVERTEX (D3DFVF_XYZ/D3DFVF_DIFFUSE)
struct CUSTOMVERTEX
{
FLOAT x, y, z;
DWORD color;
};
Будем использовать не преобразованный тип вершин, т.к. преобразования будем делать матрицами.
Изменяем код функции InitDirectX(). В эту функцию необходимо добавить установку двух режимов отображения.
Отключаем режим отсечения для того, чтобы при вращении можно было видеть все стороны объекта:
pDirectDevice->SetRenderState(D3DRS_CULLMODE, D3DCULL_NONE);
На данный момент мы не пользуемся освещением, а закрашиваем вершины в определенный цвет, поэтому отключаем освещение:
pDirectDevice->SetRenderState(D3DRS_LIGHTING, FALSE);
Упростим наше сердце, представив его в виде трех треугольников. Будем использовать локальную систему координат.
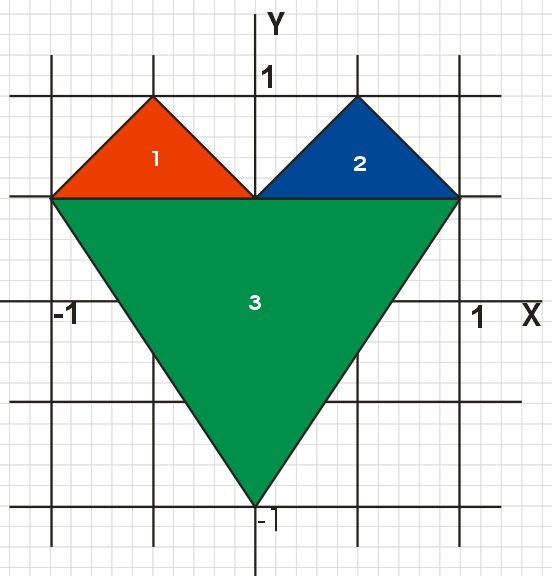
CUSTOMVERTEX stVertex[]=
{
{ -1.0f, 0.5f, 0.0f, 0x00ff0000 },
{ -0.5f, 1.0f, 0.0f, 0x00ff0000 },
{ 0.0f, 0.5f, 0.0f, 0x00ff0000 },
{ 0.0f, 0.5f, 0.0f, 0x000000ff },
{ 0.5f, 1.0f, 0.0f, 0x000000ff },
{ 1.0f, 0.5f, 0.0f, 0x000000ff },
{ -1.0f, 0.5f, 0.0f, 0x0000ff00 },
{ 1.0f, 0.5f, 0.0f, 0x0000ff00 },
{ 0.0f, -1.0f, 0.0f, 0x0000ff00 },
};
3. Создание матриц преобразования
Напишем в файле render.h функцию SetupMatrix() в которой будут происходить все действия над матрицами.
Создадим матрицы:
Установка мировой матрицы
Для того, чтобы объект вращался, необходимо получить системное время и каждое "мгновение" изменять угол между локальной системой координат и мировой ситемой координат. Вращать будем относительно оси Х, поэтому используем функцию D3DXMatrixRotationX. После расчета мировой матрицы необходимо применить ее значения с помощью функции SetTransform:
UINT iTime=timeGetTime()%5000; FLOAT fAngle=iTime*(2.0f*D3DX_PI)/5000.0f; D3DXMatrixRotationX(&MatrixWorld, fAngle); pDirectDevice->SetTransform(D3DTS_WORLD, &MatrixWorld);Установка матрицы вида
Устанавливаем камеру в нужном месте и направляем ее на объект
После расчета необходимо применить полученные значения:
pDirectDevice->SetTransform(D3DTS_VIEW, &MatrixView);Установка матрицы проекции
D3DXMatrixPerspectiveFovLH( - функция расчета матрицы проекции &MatrixProjection, - результат просчета D3DX_PI/4, - поле зрения в направлении оси У (в радианах) 1.0f, - коефициент сжатия 1.0f, - передний план отсечения сцены 100.0f); - задний план отсечения сцены
После просчета необходимо применить полученные значения:pDirectDevice->SetTransform(D3DTS_PROJECTION, &MatrixProjection);
Помещаем вызов функции расчета матриц в функцию отрисовки сцены RenderScene().
Запускаем на компиляцию и наблюдаем вращение :)
